I have a trig test tomorrow and once again, i have no idea what I'm doing ><
Please help me!
Find all solutions in the interval [0,2
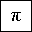 ): sec^2x-3tanx=5
): sec^2x-3tanx=5
is this what i'm supposed to do? (1/(cos^2x)-3(sinx/cosx) ?
Find all solutions in the interval [0,2
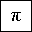 ): 1/(4sinx)
): 1/(4sinx)
Find all solutions in the interval [0,2
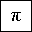 ): cos2x+sinx=0
): cos2x+sinx=0
for this one^ I assumed that I'm supposed to cahnge it to 1-sin^2x+sinx=0 but I dont know where to go from there...
Find the exact value of tan 157 degrees and 30' . (157 degrees and 30' is half of 315 degrees)
for this one... i got -1 because i used the forumla tan2u=(2tanu)/(1-tan^2u) and subsituted tan with -1 which i found on the unit circle. but my answer was undefined >< i'm supposed to get negative square root of two + one
Given cosx= -3/7 and /2 < x < , find cos (x/2)
Please help me!
Find all solutions in the interval [0,2
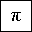
is this what i'm supposed to do? (1/(cos^2x)-3(sinx/cosx) ?
Find all solutions in the interval [0,2
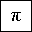
Find all solutions in the interval [0,2
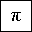
for this one^ I assumed that I'm supposed to cahnge it to 1-sin^2x+sinx=0 but I dont know where to go from there...
Find the exact value of tan 157 degrees and 30' . (157 degrees and 30' is half of 315 degrees)
for this one... i got -1 because i used the forumla tan2u=(2tanu)/(1-tan^2u) and subsituted tan with -1 which i found on the unit circle. but my answer was undefined >< i'm supposed to get negative square root of two + one
Given cosx= -3/7 and /2 < x < , find cos (x/2)
