Monkeyseat
Full Member
- Joined
- Jul 3, 2005
- Messages
- 298
1) Describe geometrically how the curve y=4^(x+3) can be transformed into the curve y=(2^x)/5 by a sequence of stretches.
Okay so I rewrote it as:
y = (4^x) * 4^3
y = (2^2x) * 64
I'm not sure now though about the stretches. Moving outwards from x this is what I did:
Horizontal stretch, scale factor 2 gives y = (2^x) * 64.
Vertical stretch, scale factor 1/64 gives y = 2^x.
Verical stretch, scale factor 1/5 gives y = (2^x)/5.
Is that correct? If not, where have I gone wrong?
2) The graph of y = f(x) is reflected in the x-axis and then the y-axis to produce the graph with equation y = g(x).
a) Find g(x) in terms of f and x.
Okay so reflection in the x-axis gives y = -f(x) and then a reflection in the y axis gives y = -f(-x).
b) Describe geometrically the single transformation that maps the graph of y = f(x) onto the graph of y = g(x).
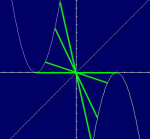
Is it a reflection in a line? Sorry, I don't know, I've drawn the graph but I can't see it:

Any help?
Thanks very much.
Okay so I rewrote it as:
y = (4^x) * 4^3
y = (2^2x) * 64
I'm not sure now though about the stretches. Moving outwards from x this is what I did:
Horizontal stretch, scale factor 2 gives y = (2^x) * 64.
Vertical stretch, scale factor 1/64 gives y = 2^x.
Verical stretch, scale factor 1/5 gives y = (2^x)/5.
Is that correct? If not, where have I gone wrong?
2) The graph of y = f(x) is reflected in the x-axis and then the y-axis to produce the graph with equation y = g(x).
a) Find g(x) in terms of f and x.
Okay so reflection in the x-axis gives y = -f(x) and then a reflection in the y axis gives y = -f(-x).
b) Describe geometrically the single transformation that maps the graph of y = f(x) onto the graph of y = g(x).
Is it a reflection in a line? Sorry, I don't know, I've drawn the graph but I can't see it:

Any help?
Thanks very much.