Transformation of a square root function with x^2 inside of it

[jmaria]

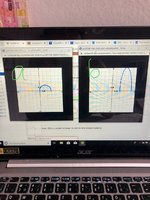
I attached the picture of the graph for f(x) (marked with an a) and the graph for g(x) (marked with a b) .
The equation for graph:a is f(x) = sqrt(3x-x^2) with this i am supposed to find the equation for graph:b as g(x) = using the transformations of graph:a

My final answer was g(x) = 4 [sqrt(3x-x^2) -2]

I came to this answer because it looked like graph:a had been vertically stretched by 4 with a horizontal shift of 2 to the right. That answer was incorrect. I realized i probably have to factor the equation for f(x) out somehow which brought me to f(x) = sqrt(x(3-x)) but i'm not sure where i could go from there to obtain the equation for g(x).

i'm comfortable with transforming graphs that have a function with an equation that contains only a square root or only x^2. But i'm lost on where to begin with equations that combine those two.

Thank you for any help!

 

[Dr.Peterson]

Before writing the complete expression for g(x), try just writing it in terms of f -- for example (not the right answer), it could be g(x) = 2f(3x+4)+5. After writing it in that form, you can use the actual expression for f. Breaking the process into these two steps can be very helpful.

Please show both steps, so I can see where you are making your mistake. I will tell you that the main error is in your placement of the 2.

 

[jmaria]

Before writing the complete expression for g(x), try just writing it in terms of f -- for example (not the right answer), it could be g(x) = 2f(3x+4)+5. After writing it in that form, you can use the actual expression for f. Breaking the process into these two steps can be very helpful.

Please show both steps, so I can see where you are making your mistake. I will tell you that the main error is in your placement of the 2.

Hello, i have

step 1: g(x) = 4f(x-2)

step 2: g(x) = 4sqrt(3x-x^2-2)

I checked to see if step 2 was correct in the system and it is saying that the domain of my function does not match the correct answer.

Thank you for the advice on how to split up the steps that made it seem more clear!

 

[Dr.Peterson]

Great! This helps a lot.

Your first step is correct; so I can see that your difficulty is in interpreting f(x-2).

The way to think of this is that you are replacing x in the definition of the function with (x-2), thought of as a single unit. This number is the input to the function.

So you are given f(x) = sqrt(3x-x^2) ; you need to replace each x with (x-2).

As an example, if I were given h(x) = x^2 + 2x, then h(x+1) would be (x+1)^2 + 2(x+1). Then I would simplify that (expanding the parentheses by distributing).

What distracted you is that the definition of f includes a function within it, and you put the "-2" in its argument, as if f(x-2) meant "put a -2 before a parenthesis", rather than doing the replacement.

Give it another try, and I think you'll get it.