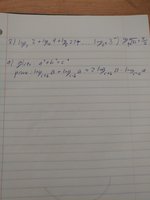Tough Problems

[Soracyn11]

I've thought about these problems alot but can't get them at all. What do you think? Please show the work I need to learn it. Help appreciated

 

[JeffM]

No one can read them, and you have shown no work.

AS YOU HAVE BEEN TOLD BEFORE

Read the page https://www.freemathhelp.com/forum/threads/read-before-posting.109846/ and then follow it.

One problem per thread.

Show what work you have done.

If you can't start, explain what you have thought about trying.

 

[Soracyn11]

Here's a cleaner copy. Im not sure where to start I would show work.

 

[Dr.Peterson]

That's still hard to read. But one way to start would be to use the change of base formula to express everything in terms of logs in one base.

Give that a try, and show some work. Or at least tell us the context of the question: What have you learned that might be relevant?

 

[Soracyn11]

Sorry forgot a parenthesis after the 8)

 

[Soracyn11]

I don't think making the base the same would help in this scenario. The log properties I've learned like multiplication of log becomes addition seems irrelevant for these problems.

 

[Soracyn11]

For the first one there seems to be a pattern of n that makes the problem equal 5/2

 

[Soracyn11]

For the second problem I tried making a, b, and c equal the square root ex: c =sqroot(a^2+b^2) but that didn't seem to help.

 

[Dr.Peterson]

I don't think making the base the same would help in this scenario. The log properties I've learned like multiplication of log becomes addition seems irrelevant for these problems.

Don't just think; do! Sometimes what you don't think will help, does, when you actually see it written out.

But if you show us any work at all, we can correct errors or suggest changes. When you just describe what you did, we can't tell where you might be going off track.

 

[Steven G]

#9

Rewrite \(\displaystyle a^2 + b^2 = c^2\) as \(\displaystyle c^2 - b^2 = (c+b)(c-b) = a^2\)

So \(\displaystyle (c+b)(c-b) = a^2\)

Then take log base (c+b) of both sides.

 

[JeffM]

With respect to the second problem, let's take an example and work it through

[MATH]a = 4,\ b = 3, \text { and } c = 5 \implies c - b = 2 \text { and } c + b = 8.[/MATH]
[MATH]log_{8}(4) + log_{2}(4) = log_2(4) + \dfrac{log_2(4)}{\log_2(8)} = 2 + \dfrac{2}{3} = \dfrac{8}{3}.[/MATH]
[MATH]2log_8(4) * log_2(4) = 2 * \dfrac{log_2(4)}{\log_2(8)} *log_2(4) = 2 * \dfrac{2}{3} * 2 = \dfrac{8}{3}.[/MATH]
The proposition is true in this case, which we found by using the change of base formula. So Dr. Peterson's suggestion has at least some promise.

 

[Dr.Peterson]

One trick I used for the second (which isn't necessary, but did help me get to something useful more quickly) is to use the fact that [MATH]log_m(n) = \frac{1}{log_n(m)}[/MATH] (an implication from the change of base formula). That immediately puts everything in terms of base a.