You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Topic: Inductive Reasoning.
- Thread starter Wilder
- Start date
lev888
Elite Member
- Joined
- Jan 16, 2018
- Messages
- 2,995
Where are you stuck?How many matches are there? If those numbers can't be seen, here they're: 1, 2, 3, 19 and 20. Also, there are 5 matches per figure.
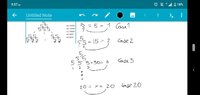
The column 1, 2, 3 must equal 5, 15, 30, respectively, by performing same operation per row. E.g. 5=5(1²) 15≠5(2²) 30≠5(3²)Where are you stuck?
Attachments
lev888
Elite Member
- Joined
- Jan 16, 2018
- Messages
- 2,995
I don't understand the above.The column 1, 2, 3 must equal 5, 15, 30, respectively, by performing same operation per row. E.g. 5=5(1²) 15≠5(2²) 30≠5(3²)
Do you see that we can start by counting the number of 5s, not matches? Let's say it's N. Then the total number of matches will be what?
Now, how do we count 5s?
How many 5s in the first row? Second? etc. See a pattern? Do you know how to calculate the sum of such sequence of numbers?
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,620
You mention triangles. Do you know about triangular numbers? If so, that's what you use. If not, you can look it up, or we can explain it.
It can also be explained in terms of arithmetic series, if you know about that.
I'm also curious about your calling this "inductive reasoning", which suggests a possible context. What have you been learning that might be of use here?
It can also be explained in terms of arithmetic series, if you know about that.
I'm also curious about your calling this "inductive reasoning", which suggests a possible context. What have you been learning that might be of use here?
lev888
Elite Member
- Joined
- Jan 16, 2018
- Messages
- 2,995
Replies to your questions.
Yes, I do. That's the question. By forming triangles. 20. 19. Nth row: 1. Yes. To be honest, no. That's why I came here.
Do you know how?
lev888
Elite Member
- Joined
- Jan 16, 2018
- Messages
- 2,995
I think it's the first 3 rows, not the 1st row. Each row has one layer.The 1st row has three layers of 5
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,620
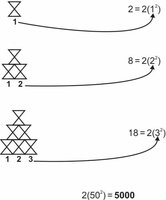
I think each row is a single row. We are shown the first three and the last two rows. And Wilder is calling each row a "column".I am missing something. The 1st row has three layers of 5, but the 20th row only has two lowers of 5. How can that be? Where does it change from three layers to two layers?
This could help a lot.You mention triangles. Do you know about triangular numbers? If so, that's what you use. If not, you can look it up, or we can explain it.
It can also be explained in terms of arithmetic series, if you know about that.
I'm also curious about your calling this "inductive reasoning", which suggests a possible context. What have you been learning that might be of use here?
Attachments
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,620
Are you saying that this is an example you were given, to show what you have been learning?This could help a lot.
It looks like you are expected just to guess at a pattern, and just confirm it (as far as you can) by testing additional cases (that might be the inductive reasoning). But with no words of explanation, I can't see what they are counting, as the first example doesn't have 2 of anything.
I do see why you seem to have made a bad guess in your post #3. Don't just imitate what they said; do (in some sense) what they did!
But you can just do what Jomo suggested in post #12, without needing a formula!