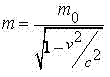You're on the right track. This is basic relativity. The rest mass of a particle as is the mass of the particle as measured in the instantaneous rest frame of the particle. The rest mass is the \(\displaystyle m_{0}\).
As our velocity approaches the speed of light, the mass becomes infinite. This says that no one can reach the speed of light because the mass becomes infinitely large. \(\displaystyle \sqrt{1-\frac{v^{2}}{c^{2}}}\) is called the Lorentz factor.
Here is a cool way to look at it.
\(\displaystyle m=\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}={\gamma}m_{0}\)........[1]
Now, consider the binomial expansion, which is valid for |x|<1,
\(\displaystyle (1+x)^{n}\sim 1+nx\)
If n=-1/2:
\(\displaystyle (1-x)^{\frac{-1}{2}}\sim 1+\frac{x}{2}\)
Let \(\displaystyle x=\frac{v^{2}}{c^{2}}\) and sub into [1]:
\(\displaystyle m=\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}\sim m_{0}\left(1+\frac{1}{2}\frac{v^{2}}{c^{2}}\right)\sim m_{0}+\frac{1}{2}m_{0}\frac{v^{2}}{c^{2}}\)
multiply through by c^2 and we can relate the relativistic energy to the rest mass energy plus the Newtonian energy of the particle:
\(\displaystyle mc^{2}=m_{0}c^{2}+\frac{1}{2}m_{0}v^{2}\).
Cool, huh?.
Imagine a space ship traveling faster and faster and approaching the speed of light. The closer it gets, its mass becomes infinite. A basic tenet of relativity. Hence \(\displaystyle E=mc^{2}\). That is why the Enterprise has to be in a Warp Bubble