BigGlenntheHeavy
Senior Member
- Joined
- Mar 8, 2009
- Messages
- 1,577
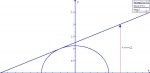
\(\displaystyle The \ figure \ shows \ a \ lamp \ located \ three \ units \ to \ the \ right \ of \ the \ y-axis \ and \ a\)
\(\displaystyle shadow \ created \ by \ the \ elliptical \ region \ x^2+4y^2 \ = \ 5. \ If \ the \ point \ (-5,0) \ is \ on\)
\(\displaystyle the \ edge \ of \ the \ shadow, \ how \ far \ above \ the \ x-axis \ is \ the \ lamp \ located?\)
[attachment=0:3ibb9tb8]AAA.JPG[/attachment:3ibb9tb8]
\(\displaystyle shadow \ created \ by \ the \ elliptical \ region \ x^2+4y^2 \ = \ 5. \ If \ the \ point \ (-5,0) \ is \ on\)
\(\displaystyle the \ edge \ of \ the \ shadow, \ how \ far \ above \ the \ x-axis \ is \ the \ lamp \ located?\)
[attachment=0:3ibb9tb8]AAA.JPG[/attachment:3ibb9tb8]