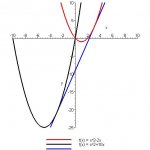
I have to find k such that the line is tangent to the graph of the function.
given f(x) = x^2 - kx. with line given y = 4x - 9
my reasoning is that i need to take the derivative first.... and so i get
f'(x) = 2x - k
after this I'm not sure how to proceed or if I should even be finding the derivative first.
given f(x) = x^2 - kx. with line given y = 4x - 9
my reasoning is that i need to take the derivative first.... and so i get
f'(x) = 2x - k
after this I'm not sure how to proceed or if I should even be finding the derivative first.