tangent line

[dannatyler]

Another question:
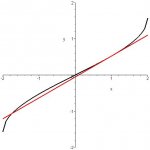
Find the equation of the tangent line to the graph of y=arcsin (x/2) at the point where x=1.

This is what I got so far but I'm not sure if I'm right:
F(1) = arcsin (1/2) F(1) = pi/6
y'= 1/2 sqrt(1-x^2/4)
m= 1/2 sqrt (1-1/4) = sqrt 3/3

equation would be y=sqrt3/3(x-1)+pi/6????? Doesn't seem correct...

 

[BigGlenntheHeavy]

\(\displaystyle given: \ f(x) \ = \ arcsin(x/2), find \ equation \ of \ tangent \ line \ to \ f(x ) \ when \ x \ = \ 1.\)

\(\displaystyle f(1) \ = \ \pi/6\)

\(\displaystyle f'(x) \ = \ \frac{1}{\sqrt{4-x^2}} \ = \ m\)

\(\displaystyle f'(1) \ = \ \sqrt3/3 \ = \ m\)

\(\displaystyle y-\pi/6 \ = \ (\sqrt3/3)(x-1)\)

\(\displaystyle y \ = \ (\sqrt3/3)(x-1)+\pi/6, \ see \ graph.\)

[attachment=0:m2bza2ni]xyz.jpg[/attachment:m2bza2ni]

 

[dannatyler]

just one question for. Isn't Y'= 1/2sqrt(1-x^2/4)?

 

[Deleted member 4993]

just one question for. Isn't Y'= 1/2sqrt(1-x^2/4)? It is.

Instead of staring at the solution - get a paper and pencil and work through it.

Spoiler: :28y2mocx

\(\displaystyle \frac{1}{2\sqrt{1-(\frac{x}{2})^2}} \ \ = \ \ \frac{1}{2\sqrt{\frac{4-x^2}{4}}} \ \ = \ \ \frac{1}{\sqrt{4-x^2}}\)[/spoiler:28y2mocx]

 

[BigGlenntheHeavy]

\(\displaystyle D_x[arcsin(x/2)] \ = \ \frac{1/2}{\sqrt{1-x^2/4}} \ = \ \frac{1/2}{\sqrt{4-x^2}/2}\)

\(\displaystyle = \ \ \bigg(\frac{1}{2}\bigg)\bigg(\frac{2}{\sqrt{4-x^2}}\bigg) \ = \ \frac{1}{\sqrt{4-x^2}}\)