Tangent Line with derivative of trig functions

[asimon2005]

Calculus: Early Transcendentals by James Stewart
d= dy/dx (sin x) = cos x
d= dy/dx (cos x)= -sin x
d= dy/dx (tan x)= sec^2 x
d= dy/dx (csc x) = -csc x tan x
d= dy/dx (sec x) = sec x tan x
d= dy/dx (cot x) = -csc^2 x

Find an equation of the tangent line to the curve at the given point.

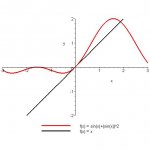
52. y = sin x + sin^2 x (0,0)
Is it y' = cos x + cos^2 x or y' = cos x + 2sinxcosx


54. y= x^2e^-x (1,1/e) the equation y= reads x squared times e to the -x if you were wondering.

I just need help with these problems.

P.S. those are points in which I surrounded by parenthesis.

 

[galactus]

Find an equation of the tangent line to the curve at the given point.

52. y = sin x + sin^2 x (0,0)
Is it y' = cos x + cos^2 x or y' = cos x + 2sinxcosx

It's the last one.
Differentiate \(\displaystyle \frac{d}{dx}[sin(x)+sin^{2}(x)]=(2sin(x)+1)cos(x)\)

Now, to find the slope, m, at the point (0,0) plug in x=0. We find m=1.

Now, use y=mx+b. Plug in m=1, x=0, y=0 and solve for b. You're done.

 

[BigGlenntheHeavy]

Here's what the plot looks like for 52.

[attachment=0:dntpedtb]kkk.jpg[/attachment:dntpedtb]