summer homework help

[sashanl]

i need help on this summer homework.

i don't know how to do this, so any advice, help, or showing steps/work would be great
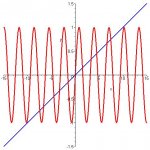
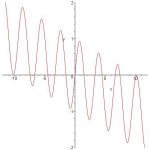
- How many times does the graph of y = 0.1x intersect the graph of y = sin(2x)? Justify your answer

i did this problem, but want to know if my answer is correct, or if there are more steps
- simplify:[ 1/(3+x) - 1/2 ]/x


so i got[ 2 - (2+x) ]/ [ 2(x)(2+x) ]

i don't know how to do this one
- evaluate the limit: lim x-> infinity (7-x^3)/(x+6)

 

[BigGlenntheHeavy]

First one: See graph below.

Now how many times does the blue line (y=.1x) intersect the red equation (y = sin(2x)?

[attachment=0:rdudfdmt]nnn.jpg[/attachment:rdudfdmt]

 

[sashanl]

THANK YOU SO MUCH!

 

[fasteddie65]

evaluate the limit: lim x-> infinity (7-x^3)/(x+6)

Notice that the degree of the numerator (3) is greater than the degree of the denominator (1), so there is no limit. Or yo could say -?, since the numerator has a negative coefficient on the x^3 and the denominator has a positive coefficient on the x.

 

[mmm4444bot]

See graph below.

Now how many times does the blue line (y=.1x) intersect the red equation (y = sin(2x)?

From looking at that graph alone, I'm not sure. :wink:


[attachment=0:1ask5m5o]not_sure.JPG[/attachment:1ask5m5o]

 

[BigGlenntheHeavy]

11 times, at around x = ± 10, close, but no cigar.

 

[daon]

\(\displaystyle \sin2x\) has period \(\displaystyle \pi\) and amplitude 1.

First note on what interval \(\displaystyle -1 \le 0.1x \le 1\), that would be \(\displaystyle [-10, 10]\)

Now you need to count the number of turns in \(\displaystyle [0,10]\)

\(\displaystyle 2cos2x = 0 \iff x = (\frac{\pi}{4} + \pi i) \,\,\,\, or \,\,\,\, x = (\frac{3\pi}{4} + \pi j)\)

From here we can determine \(\displaystyle x\in [0,10] \iff i=0,1,2,j=0,1,2\)

We can do the same for the the other side of the y axis and get 6 also. However, we are double-counting the origin. So as said above, the answer is 12-1=11.

You must be careful with this analysis in general, since we can have a turning point without an intersection or vice-versa. But since we have \(\displaystyle (sin2x)' = 2cos2x > 0\) when x is "close to" \(\displaystyle \pm 10\) in this interval and \(\displaystyle 0.1x > sin(2x)\) after the last turning point, we won't over- or under-count.

 

[BigGlenntheHeavy]

If one graphs f(x) = sin(2x) - .1x, it is readily apparent that there are exactly 11 solutions.

[attachment=0:1ooo3ez5]http://www.jpg[/attachment:1ooo3ez5]

 

[mmm4444bot]

If one graphs f(x) = sin(2x) - .1x, it is readily apparent that there are exactly 11 solutions.

Ah, an intellectual "retooling" of machine results. Good one!

(Boeing could use more people like Glenn.)