Summation Getting from here to there
- Thread starter seal308
- Start date
What did you get when you followed the standard steps of induction? For instance, you started by testing the case n = 2:
\(\displaystyle T(2) = 1 = \dfrac{(2-1)(1)}{2} = \dfrac{2}{2} = 1\)
Because that checked out, you then assumed it true for n = k, and attempted to prove it for n = k + 1:
\(\displaystyle T(k+1) = k + (k - 1) + (k-2) + ... + 1 = k + T(k) = k + \dfrac{(k-1)(k)}{2}\)
...and then what? Please share with us any and all work you've done on this problem, even the parts you know for sure are wrong. Thank you.
\(\displaystyle T(2) = 1 = \dfrac{(2-1)(1)}{2} = \dfrac{2}{2} = 1\)
Because that checked out, you then assumed it true for n = k, and attempted to prove it for n = k + 1:
\(\displaystyle T(k+1) = k + (k - 1) + (k-2) + ... + 1 = k + T(k) = k + \dfrac{(k-1)(k)}{2}\)
...and then what? Please share with us any and all work you've done on this problem, even the parts you know for sure are wrong. Thank you.
Hi,
My textbook shows me this:
And tells me that it is derived by this:
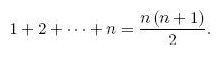
which was proven by induction.
I just don't get how they did > > > that. < < <
seal308, your use of the word "that" makes your post unclear as to whether you were referring to the induction itself or
how the formula was derived from the other formula. Which did you mean?
Apologies for being unclear.
The textbook has already proven this first expression by induction:
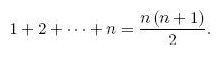
It then tells me that this second expression:
Was derived from the first expression.
I don't think it's asking me to prove the second expression by induction.
It just simply told me that it was derived from the first.
I don't understand how they went from this:
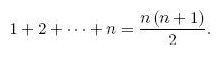
To this:
Again I don't think it's asking me to prove it by induction.
I think it's saying that you somehow modify the first expression to get the second one and I don't know how to do that.
It may be widely known but I'm just learning it.
And again, as I've explicitly stated twice, the textbook has already proven that so I'm not even questioning it.
Your response makes me question if I'm in the right place.
Perhaps this is a too advanced section.
Am I in the right section of this forum?
Should I be posting this in a different section?
Well, alright. So you're saying you accept the proof given of the first, but you're having trouble seeing how the second given equation is related. That's fair, and I think part of the problem might be that they reversed the order of the terms on you and that threw you for a loop. Let's start by designating the function we know to be true as F(n):
\(\displaystyle F(n)=1+2+3+...+n=\dfrac{n(n+1)}{2}\)
Because T(n) is a function only using addition, which is commutative, we can freely move around the terms without changing its value. So let's fully reverse the order of the terms so it becomes:
\(\displaystyle T(n)=1+2+3+...+n-1\)
From this, we can clearly see that, for any positive integer n >= 2, T(n) = F(n-1). If we plug in the value n-1 to the original function then we can see that it becomes the very statement the book tells us it is.
\(\displaystyle T(n)=F(n-1)=\dfrac{(n-1)((n-1)+1)}{2}=\dfrac{(n-1)n}{2}\)
\(\displaystyle F(n)=1+2+3+...+n=\dfrac{n(n+1)}{2}\)
Because T(n) is a function only using addition, which is commutative, we can freely move around the terms without changing its value. So let's fully reverse the order of the terms so it becomes:
\(\displaystyle T(n)=1+2+3+...+n-1\)
From this, we can clearly see that, for any positive integer n >= 2, T(n) = F(n-1). If we plug in the value n-1 to the original function then we can see that it becomes the very statement the book tells us it is.
\(\displaystyle T(n)=F(n-1)=\dfrac{(n-1)((n-1)+1)}{2}=\dfrac{(n-1)n}{2}\)