TedChirvasiu
New member
- Joined
- Jun 29, 2013
- Messages
- 6
Hey there!
I was wondering if anyone could, please, help me find a solution for the following problem :
We have a variable S, which can be any rational number... (I know the value of S)
Say we the following sum : (Condition 1) 4n*k0 + 4n-1*k1 + ... + 40*kn = C where C > 0 and (Condition 2) k0 + k1 + ... + kn = 2x (Where x is a known integer)
Now the question is : How can i get the values of all the k's so that C is the largest sum that can fit into S?
Let's take an example :
For instance,
S = 251,2151
n = 10
x = 4 (So k0 + k1 + ... + k10= 16)
In this case, anything above n=3 should have its k equal to 0, since they are larger than 251 alone (and remember, the sum of the factors has to be 16).
So the remaining possibilities are 1,4,16,64. Therefore k10-0 + k10-1 + k10-2 + k10-3 = 16 (Since anything above k4 is 0) and C = 40*k10-0 + 40*k10-1 + 40*k10-2 + 40*k10-3 . How can i get the 4 k's so that C is the largest sum smaller or equal to S?
Could anybody help me with this, please? It looks like some sort of geometrical progression, but those k's really complicate the things... My maths teacher said it could probably be solved with combinatorics or something but couldn't give me an answer... Sorry if it sounds ambiguous, i could explain further if needed...
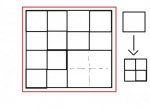
This is what i'm really trying to do : Imagine S is the surface of a square (Red in the picture), then you have a bunch of smaller squares (black) that can be divided into 4 smaller squares. So the surface of a divided square is 4 times smaller than its parent. If i have a limited number of squares (in our case, the 2x thing), regardless of their division steps, what is the number of each divided chunk (the k's) i can fit in the red square so that i almost fill the entire thing? (Again, respecting precisely the limit of chunks. No more, no less)
Any kind of help would be greatly appreciated!
Thanks in advance!
I was wondering if anyone could, please, help me find a solution for the following problem :
We have a variable S, which can be any rational number... (I know the value of S)
Say we the following sum : (Condition 1) 4n*k0 + 4n-1*k1 + ... + 40*kn = C where C > 0 and (Condition 2) k0 + k1 + ... + kn = 2x (Where x is a known integer)
Now the question is : How can i get the values of all the k's so that C is the largest sum that can fit into S?
Let's take an example :
For instance,
S = 251,2151
n = 10
x = 4 (So k0 + k1 + ... + k10= 16)
In this case, anything above n=3 should have its k equal to 0, since they are larger than 251 alone (and remember, the sum of the factors has to be 16).
So the remaining possibilities are 1,4,16,64. Therefore k10-0 + k10-1 + k10-2 + k10-3 = 16 (Since anything above k4 is 0) and C = 40*k10-0 + 40*k10-1 + 40*k10-2 + 40*k10-3 . How can i get the 4 k's so that C is the largest sum smaller or equal to S?
Could anybody help me with this, please? It looks like some sort of geometrical progression, but those k's really complicate the things... My maths teacher said it could probably be solved with combinatorics or something but couldn't give me an answer... Sorry if it sounds ambiguous, i could explain further if needed...
This is what i'm really trying to do : Imagine S is the surface of a square (Red in the picture), then you have a bunch of smaller squares (black) that can be divided into 4 smaller squares. So the surface of a divided square is 4 times smaller than its parent. If i have a limited number of squares (in our case, the 2x thing), regardless of their division steps, what is the number of each divided chunk (the k's) i can fit in the red square so that i almost fill the entire thing? (Again, respecting precisely the limit of chunks. No more, no less)
Any kind of help would be greatly appreciated!
Thanks in advance!
Attachments
Last edited: