Substitution in Multiple Integrals

[kitarzan]

Hi, I am having some difficulty with the following problem:

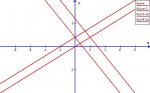
The region R is bounded by the lines y=x, y=x+2, y=2-2x, and y=6-2x. Find the mass of this lamina if the density(x,y)=4x^2+4xy+y^2 g/cm^3.

This problem is supposed to be solved using a substitution to transform the region R into a region G in the uv-plane. I have sketched the region R in the xy-plane and have found the intersections of the boundry functions but I do not know how to find the appropriate functions x=g(u,v) and y=h(u,v) to complete the transformation. Any help would be appreciated.

Thanks!
Kit

 

[galactus]

Let's rewrite the line equations as:

\(\displaystyle y-x=0, \;\ y-x=2, \;\ y+2x=2, \;\ y+2x=6\)

See now what u and v subs to make?.

Let \(\displaystyle u=y-x, \;\ v=y+2x\)

Solving these for x and y in terms of u and v gives:

\(\displaystyle x=\frac{v-u}{3}, \;\ y=\frac{2u+v}{3}\)

Now, find the partials and solve the determinant. I will use d for \(\displaystyle {\partial}\) for less typing.

\(\displaystyle \Large\begin{vmatrix}\frac{dx}{du}&\frac{dx}{dv}\\ \frac{dy}{du}&\frac{dy}{dv}\end{vmatrix}=\begin{vmatrix}\frac{-1}{3}&\frac{1}{3}\\ \frac{2}{3}&\frac{1}{3}\end{vmatrix}=\frac{-1}{3}\)

Note that \(\displaystyle 4x^{2}+4xy+y^{2}=(2x+y)^{2}=v^{2}\)

\(\displaystyle \frac{1}{3}\int_{2}^{6}\int_{0}^{2}v^{2}dudv\)

Now, can you solve?. I have included a graph of the region pre-transformation and post-transformation

 

[kitarzan]

Thanks! I can't believe I got stumped on that one. Makes perfect sense now.