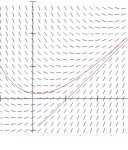
Hey people, I'm working on some math problems and I ran into one that asks me to determine the straight-line solution of the equation from the direction field.
The equation is y' = t - y and a graph of the field and a couple of curves is attached to this post.
Is the straight-line solution where the curve appears to be a straight line?
The equation is y' = t - y and a graph of the field and a couple of curves is attached to this post.
Is the straight-line solution where the curve appears to be a straight line?