Spiral with variable radius

[Wouter]

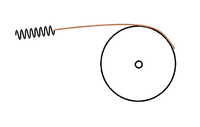
For university we've got to build a small vehicle powered by two tension springs. Since a wheel and these springs have different motions; conversion from a linear to rotary motion is done by attaching a belt to a wheel and the spring in order for all the spring forces to be converted into tangential forces as pictured in the attached image.
The force from the spring can be described as: F = c * u
where F = force [N], c = spring constant [N/mm], u = extension spring [mm]. The maximum extension of the spring is 118 mm and the spring constant is 0.4 N/mm.
The torque as reaction of the spring can be described as: T = F * r
where T = Torque [Nmm], F = force [N] and r = radius of the wheel [mm]
Substitution gives:
T = (c * u) * r
Considering we want a constant torque (500 Nmm) and the force is dependent on the length of the spring; only the radius is variable we get the following:
r = T / (c * u) -> r(0 < u < 118) = 500 / (0.4 * u)
Ofcourse this is a reciprocal function with an asymptote where u = 0.

Since the maximum arc length of the spiral equals the maximum spring length, I thought I could get a variable angle (theta) with the circle circumference equation:
c = r * theta
where c = circumference [mm], r = radius of the wheel [mm] and theta = angle [rad]. c = 118 and r is known from the last equations. substitution gives:
theta (0 < u < 118) = 118 * (0.4*u/500)

Eventually the parametric equation for a circle is:
F (theta) = (x(theta), y(theta))
x (theta) = r * cos (theta)
y (theta) = r * sin (theta)

substituting the previous values gives:

F (0 < u < 118)= (x(u), y(u))
x (u) = (500/(0.4*u)) * cos (118*(0.4*u/500))
x (u) = (500/(0.4*u)) * sin (118*(0.4*u/500))

However my results may look correct (at least its a spiral starting at a radius of around 10) the increasing radius and the arc length (I'm checking my arc length with SolidWorks evaluation tools) are not.
What am I doing wrong? Is there a better way?

 

[Cubist]

Since the maximum arc length of the spiral equals the maximum spring length, I thought I could get a variable angle (theta) with the circle circumference equation:
c = r * theta
where c = circumference [mm], r = radius of the wheel [mm] and theta = angle [rad]. c = 118 and r is known from the last equations. substitution gives:

I think you went wrong in the above quoted section, since r is not constant. This is a spiral, not a circle!

Since u can't be zero (there must be a minimum extension of the spring to produce a torque) then

Let u go from u₀ → u₁ as θ goes from 0 → 2π

where u₀ is to be determined and u₁=118

Perhaps consider a small arc length, du = r dθ. This is heading towards performing an integral, with certain limits, that should help you to determine u₀ (hopefully u₀ will be greater than 0 otherwise you'll have to rethink the mechanics, perhaps using two springs maybe)

 

[Wouter]

You're absolutely right.

However, I messed around a little bit. But it's impossible to get these radii with the arc length I need when the spring is getting shorter.
Bottom line; I dropped the idea partially. Since It began as a rather "Linear" function, I used an archimedean spiral for about 80% of the spring length and it works out.

Anyways, thank you for you time!