Speed of Shadow

[turophile]

Here's the problem:

A man 6 feet tall is walking at 4 feet per second away from a pole 15 feet high. There is a light at the top of the pole. How fast is the far end of the man's shadow moving?

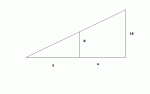
I drew a picture and assigned some variables to the various distances:

Let:
a = height of the pole
b = distance from base of the pole to the far end of the man's shadow
c = distance from light to the far end of man's shadow
d = distance from the base of the pole to the man's feet
e = distance from the man's feet to the far end of the man's shadow
f = distance from the light to the man's head
g = distance from the man's head to the far end of the man's shadow
h = distance from the man's feet to the man's head
i = distance from the light to the man's feet

We know that:
b = d + e
c = f + g
a[sup:v2nawna3]2[/sup:v2nawna3] + b[sup:v2nawna3]2[/sup:v2nawna3] = c[sup:v2nawna3]2[/sup:v2nawna3]
h[sup:v2nawna3]2[/sup:v2nawna3] + e[sup:v2nawna3]2[/sup:v2nawna3] = g[sup:v2nawna3]2[/sup:v2nawna3]
a[sup:v2nawna3]2[/sup:v2nawna3] + f[sup:v2nawna3]2[/sup:v2nawna3] = i[sup:v2nawna3]2[/sup:v2nawna3]

We are given a = 15 ft., h = 6 ft., and df/dt = 4 ft./sec.

We want to know dc/dt.

I'm not sure what the next step should be, though.

 

[galactus]

It would appear you have a few too many variables

This problem is not that involved. It is just a similar triangle.

Per the diagram \(\displaystyle \frac{15}{x+y}=\frac{6}{y}\Rightarrow y=\frac{2x}{3}\)

Differentiate:

\(\displaystyle \frac{dy}{dt}=\frac{2}{3}\cdot\frac{dx}{dt}\)

You are given dx/dt=4. You need dy/dt (y is the man's shadown length, thus dy/dt is its change in length).

 

[turophile]

Many thanks. Sorry I didn't explain all the variables. There are other parts to the problem that I didn't post that needed some of the other variables.

One question: The solution of dy/dt in the similar triangle model you gave is 8/3 ft./sec. However, the answer in my textbook to the part of the problem I posted here is 20/3 ft./sec. But it gives 8/3 ft./sec. as the solution to another part of the same problem, which is "How fast is the length of the shadow increasing?" So does the 20/3 ft./sec. come from dx/dt + dy/dt = 4 ft./sec. (the man's speed) + 8/3 ft./sec. (the speed of the shadow's growth)?

 

[Deleted member 4993]

Many thanks. Sorry I didn't explain all the variables. There are other parts to the problem that I didn't post that needed some of the other variables.

One question: The solution of dy/dt in the similar triangle model you gave is 8/3 ft./sec. However, the answer in my textbook to the part of the problem I posted here is 20/3 ft./sec. But it gives 8/3 ft./sec. as the solution to another part of the same problem, which is "How fast is the length of the shadow increasing?" So does the 20/3 ft./sec. come from dx/dt + dy/dt = 4 ft./sec. (the man's speed) + 8/3 ft./sec. (the speed of the shadow's growth)?.... Yes

Referring to Galactus' diagram - say

O = base of the lamp post

M = Tip of the shadow

Then

OM = x + y

\(\displaystyle \frac{d}{dt}OM \ \ = \ \ \frac{dx}{dt} \ \ + \ \ \frac{dy}{dt}\)