Someone goes N, someone goes S, moving apart how fast?

[dangerous_dave]

A man starts walking north at 4 km/hr from a point P. 15 minutes later, a woman starts walking south at 5 km/hr from a point 2km due east of P. At what rate are the people moving apart 6 minutes after the woman starts walking?

I need help getting started, I don't really know where to begin.

 

[skeeter]

let point P be the origin.

man's position (x,y) as a function of time is \(\displaystyle (0, 4t)\), where t is in hours.

woman's position (x,y) as a function of time is \(\displaystyle \left(2, -5\left(t - \frac{1}{4}\right)\right)\)

let z = distance between them. using the distance formula ...

\(\displaystyle z = \sqrt{(0-2)^2 + \left[4t + 5\left(t - \frac{1}{4}\right)\right]^2}\)

simplify z a bit, then differentiate to find \(\displaystyle \frac{dz}{dt}\)

 

[stapel]

I need help getting started, I don't really know where to begin.

Draw a picture, and look for right triangles! :wink:

Eliz.

 

[dangerous_dave]

Thanks that helps heaps. Im having a bit of trouble with the simplifying. Does it follow the rules to simplify to this?

z = 2 + sqrt(4t) + 5(t-1/4)

Or does that break the rules?

@ stapel: I did, and puting that with skeeters help, I worked out how skeeter got to that point. Now just the differentiation...

 

[skeeter]

Thanks that helps heaps. Im having a bit of trouble with the simplifying. Does it follow the rules to simplify to this?

z = 2 + sqrt(4t) + 5(t-1/4)

Or does that break the rules? your algebra for simplifying z is incorrect ... follow the order of operations inside the radical first. you should get

\(\displaystyle z = \sqrt{81t^2 - \frac{45}{2} t + \frac{89}{16}}\)

 

[dangerous_dave]

Oh of course thanks

 

[galactus]

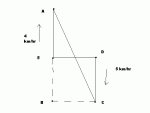
Let's try it this way.

After the woman has walked 6 miutes, the man has walked 21 minutes. Therefore, he has walked (4)(21/60)=7/5 km

The woman has walked 5(6/60)=1/2 km.

From triangle ABC, The distance between them(AC) at 6 minutes after she starts walking is \(\displaystyle \sqrt{(19/10)^{2}+(2)^{2}}=\frac{\sqrt{761}}{10}\)km.

So, we can use ol' Pythagoras:

\(\displaystyle D^{2}=x^{2}+y^{2}\)

\(\displaystyle D\frac{dD}{dt}=x\frac{dx}{dt}+y\frac{dy}{dt}\)

They are moving apart vertically at dy/dt=4+5=9 km/hr. Since the distance between them stays at 2 km, then dx/dt=0.

\(\displaystyle D=\frac{\sqrt{761}}{10}, \;\ x=2, \;\ dx/dt=0, \;\ y=19/10, \;\ dy/dt=9\)

\(\displaystyle (\frac{\sqrt{761}}{10})\frac{dD}{dt}=2(0)+(\frac{19}{10})(9)\)

\(\displaystyle \frac{dD}{dt}=\frac{171}{\sqrt{761}}\approx{6.2} \;\ km/hr\)

I think this is a little easier since we do not have to deal with radicals in our differentiation.

For the previous method, \(\displaystyle \frac{dD}{dt}=\frac{1}{2}\cdot\frac{162t+18}{\sqrt{81t^{2}+18t+5}}\)

Now, if you plug in t=1/10, you should get the same result.