Hey there, this forum seems pretty dead, so I thought that I'd give you guys some math challenges to do.
1. For a regular 12-sided polygon (dodecagon), how many diagonals (a diagonal is a line that connects two points within the polygon, sides are not diagonals) can you draw inside the figure? Solved by Denis
1.1. How many triangles can be formed inside a dodecagon, where the vertices of the triangles are on the vertices of the dodecagon, and each triangle can only share a maximum of one side with the dodecagon?
2. Image a 3x5 checkerboard. The bottom left point is labeled as point A. The top right point is labeled as point B. How many ways can you go from point A to point B, if each move consists of either moving one unit up or one unit to the right. Example: moving up 3, then 5 to the right is considered a unique path.
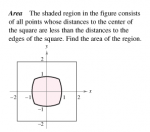
3. See attachment.
P.S. If the mods are worried that this is a homework problem, I can provide the solution, if requested.
1. For a regular 12-sided polygon (dodecagon), how many diagonals (a diagonal is a line that connects two points within the polygon, sides are not diagonals) can you draw inside the figure? Solved by Denis
1.1. How many triangles can be formed inside a dodecagon, where the vertices of the triangles are on the vertices of the dodecagon, and each triangle can only share a maximum of one side with the dodecagon?
2. Image a 3x5 checkerboard. The bottom left point is labeled as point A. The top right point is labeled as point B. How many ways can you go from point A to point B, if each move consists of either moving one unit up or one unit to the right. Example: moving up 3, then 5 to the right is considered a unique path.
3. See attachment.
P.S. If the mods are worried that this is a homework problem, I can provide the solution, if requested.
Attachments
Last edited: