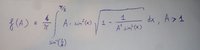Solving parametric integral
- Thread starter Pollo
- Start date
this is what mathematica returns... have fun
[MATH]\frac{\left(A^2-1\right) \left(A \left(\pi -i \log \left(2 \left(A^2-1\right)\right)\right)-\frac{\sqrt{2} \sqrt[4]{A^2-1} \log \left(2 \left(A^2-1\right)\right)}{\sqrt{i \sinh \left(2 \log \left(\frac{\sqrt{A^2-1}+i}{A}\right)\right)}}\right)}{\pi A^2}[/MATH]
[MATH]\frac{\left(A^2-1\right) \left(A \left(\pi -i \log \left(2 \left(A^2-1\right)\right)\right)-\frac{\sqrt{2} \sqrt[4]{A^2-1} \log \left(2 \left(A^2-1\right)\right)}{\sqrt{i \sinh \left(2 \log \left(\frac{\sqrt{A^2-1}+i}{A}\right)\right)}}\right)}{\pi A^2}[/MATH]
D
Deleted member 4993
Guest
Please follow the rules of posting in this forum, as enunciated at:
READ BEFORE POSTING
Please share your work/thoughts about this assignment.
Try substitution:
y = A * sin(x)
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,598
Well of course you will get a function in terms of A. Just look at the limits. Can we please see your progress so that we can help you?
Here are some steps to start with:
Can you continue to find an integral for f(A)?
You can use Wolfram to determine values for f(2), f(3), f(4), f(5), f(6), f(7).
Can you see a pattern for these values and use it to come up with a rule for f(A)?
Can you continue to find an integral for f(A)?
You can use Wolfram to determine values for f(2), f(3), f(4), f(5), f(6), f(7).
Can you see a pattern for these values and use it to come up with a rule for f(A)?
I finally solved this problem in a rather simple way by making this substitution:
[MATH]t = A\,cos(x) [/MATH][MATH]dt = -A\,sin(x)\,dx [/MATH]
and by knowing this: [MATH]\int \sqrt{a^2 - x^2} dx = \frac{x\,\sqrt{a^2-x^2}}{2} + \frac{a^2}{2}\,\sin^{-1}\left(\frac{x}{a}\right) + constant[/MATH]
It's too long to write all the steps, but by knowing these two things it is very easy.
The final result is
[MATH]f(A) = \frac{A^2-1}{A}[/MATH]
This result is in line with my expectations, being this problem related to a physical one.
Thanks everybody!
@Romsek : why does Mathematica return such a complicated result??
[MATH]t = A\,cos(x) [/MATH][MATH]dt = -A\,sin(x)\,dx [/MATH]
and by knowing this: [MATH]\int \sqrt{a^2 - x^2} dx = \frac{x\,\sqrt{a^2-x^2}}{2} + \frac{a^2}{2}\,\sin^{-1}\left(\frac{x}{a}\right) + constant[/MATH]
It's too long to write all the steps, but by knowing these two things it is very easy.
The final result is
[MATH]f(A) = \frac{A^2-1}{A}[/MATH]
This result is in line with my expectations, being this problem related to a physical one.
Thanks everybody!
@Romsek : why does Mathematica return such a complicated result??