mertz said:
i wish i knew how to get those [numerical approximations for roots of ln(x - 4) - cos(Pi*x) within 4<=x<=6]. the question does ask me to use the calculator, but i'm pretty new to my t-83, and i would rather just know how to get the answer without using the calculator (if that's possible).
I'm curious to know whether or not your instructor uses calculators in the classroom. I mean, would you expect an explicit instruction to employ a calculator, if this is what were expected?
So, I'm thinking that there is no algebraic method by formula and by hand to answer the exercise.
Glenn let the calculator do the grunt work, but you can also use your TI-83 to "assist" you, as you reason out the answer in your head.
Have you been exposed to the limit concept?
Are you familiar with the basic shape of both the log() function and a sinusoidal function?
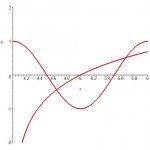
Did you make any kind of rough sketch?
So, we know that the log() function comes up from **** and crosses the x-axis somewhere relatively near the Origin (on the right), as it elegantly slows it curve of ascent, continuing up to God only knows where.
Well, there's a cosine wave straddling the x-axis. So, the log() curve also passes through the cosine wave. It's reasonable, based on the relative shapes of these types of functions, that the log() curve intersects the wave more than once.
So, we don't know the location of the first point of intersection within the interval [4, 6], but we can evaluate each function at the endpoints of this restricted domain, so that we can at least know which function is "on top" (i.e., which function is greater than the other between x = 4 and x = 1st intersection and which function is "on top" between x = the last point of intersection and x = 6).
Note: The notation log() means the natural logarithm, from here on out.
L(x) = log(x - 4)
C(x) = cos(Pi*x)
We can't evaluate L(4) because it's undefined! But we can get as close to the number L(4) as we like: L(4.01) L(4.001) L(4.0001) et cetera.
L(4.01) = -4.6 [rounded]
Of course, the cosine of even multiples of Pi is 1, so that's easy.
C(Pi*4) = 1
Obviously, as the two functions are located just inside the restricted zone, at x = 4, the cosine wave is "on top" (i.e., the value of y = 1 is greater than the value of y = -4.6).
Using the same approach, to see what's happen'n where the functions exit the restricted zone gives more information.
Now comes the grunt work. Use the calculator to help you build a chart of the values of y for each, as they come closer together. You can zero-in on the first point of intersection sufficiently close to know when you've passed it, by examining the numerical data in your xy-chart for both functions L and C, as x goes from 4 to 6.
With 20 minutes of experimenting, refining rougher sketches into less-rough sketches, pluggin' and chuggin' out values for y, and using this quasi-limit approach to get a sense of how many and where the intersections are, we can do it, if our pre-requisite knowledge and skills are good.
I mean, after all, you did start by going to a computer program and typing in the info (albeit, incorrectly). What did you do with paper and pencil first, since the exercise does not instruct you to use technology? (That's a "rhetorical"

)
Cheers ~ Mark