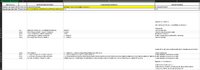
To begin with, I want to clarify that the question concerns EXPECTED values, not historical. This is my first ever post here, so please don't be offended if I use Excel notation.
The formula for expected geometric return of an asset class, when given expected arithmetic return and expected standard deviation is as follows:
GR = EXP(LN(1+AR)-0.5*LN(1+(STDEV/(1+AR))^2))-1
where:
GR = Expected Geometric Return
AR = Expected Arithmetic Return
STDEV = Expected St. Dev.
I have also come across the following formula for expected arithmetic return, when given expected geom. return and exp. st. dev.
AR = (1+GR)*SQRT(0.5+(0.5*SQRT((1+((4*$STDEV^2)/(1+GR)^2)))))-1
My question is how to solve for AR when GR and STDEV are provided. The attached snapshot illustrates my failed attempts to simplify the first equation and solve for AR. Any help and ideally step by step solution would be greatly appreciated.
The formula for expected geometric return of an asset class, when given expected arithmetic return and expected standard deviation is as follows:
GR = EXP(LN(1+AR)-0.5*LN(1+(STDEV/(1+AR))^2))-1
where:
GR = Expected Geometric Return
AR = Expected Arithmetic Return
STDEV = Expected St. Dev.
I have also come across the following formula for expected arithmetic return, when given expected geom. return and exp. st. dev.
AR = (1+GR)*SQRT(0.5+(0.5*SQRT((1+((4*$STDEV^2)/(1+GR)^2)))))-1
My question is how to solve for AR when GR and STDEV are provided. The attached snapshot illustrates my failed attempts to simplify the first equation and solve for AR. Any help and ideally step by step solution would be greatly appreciated.