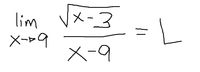Solving equation with radicals

[marmar2128]

Hi guys, im new here btw.

I tried to solve this problem but i was quite confused with a radical of the equation.

√x-3/x-9

I conjugated it.

√x-3/x-9●√x+3/√x+3 = 1/x-9(√x+3).

From here, i was stucked because of the denominator. I have no idea what to do next. Is it already simplified or there are more to do? Or am I wrong at the first place?

Thanks in advance.

 

[MarkFL]

Hello, and welcome to FMH!

It appears you are to simplify a rational expression:

[MATH]\frac{\sqrt{x}-3}{x-9}[/MATH]
If I am interpreting your expression correctly, which I would have written as:

(√(x) - 3)/(x - 9)

if I weren't using \(\LaTeX\), then what I would do is observe that:

[MATH]x-9=(\sqrt{x})^2-3^2=(\sqrt{x}+3)(\sqrt{x}-3)[/MATH]
Can you proceed?

 

[marmar2128]

Oh no, sorry but the √x-3 i mentioned is not only the x should be squared but the √x-3 as a whole. I multiplied the conjugate of √x-3, which is √x+3 so the answer in the numerator to be 1. But on the denominator it appears that i cant multiply x-9 to √x-3 because it is a radical binomial. Is there a way to simplify the denominator or just stay as it is?

Or somethings not right at the way i solve my equation?

 

[MarkFL]

What is the complete problem, and the instructions preceding it? The image you uploaded is sideways, likely because you are using a phone.

 

[marmar2128]

oh im very sorry. i resorted to ms paint and write the equation there. we took lessons about limits.
can you please solve this for me? this will be my reference about radicals.

 

[MarkFL]

That limit is unbounded, as we have a finite value in the numerator and zero in the denominator. I suspect it is supposed to be:

[MATH]L=\lim_{x\to9}\frac{\sqrt{x}-3}{x-9}=\lim_{x\to9}\frac{1}{\sqrt{x}+3}=\frac{1}{6}[/MATH]

 

[JeffM]

This is the same as Mark's answer, but with his points in posts 2 and 6 brought together.

[MATH]x \ne 9 \implies \dfrac{\sqrt{x} - 3}{x - 9} = \dfrac{\sqrt{x} - 3}{(\sqrt{x} - 3)(\sqrt{3} + 3)} = \dfrac{1}{\sqrt{x} + 3}.[/MATH]
[MATH]x = 9 \implies \dfrac{1}{\sqrt{x} + 3} = \dfrac{1}{\sqrt{9} + 3} = \dfrac{1}{6}.[/MATH]
Now it should be easy to demonstrate that

[MATH]\lim_{x \rightarrow 9}\dfrac{\sqrt{x} - 3}{x - 9} = \dfrac{1}{6}.[/MATH]

 

[Otis]

… i resorted to ms paint and write the equation there …

Hi marmar. If you've posted the function as given, then the limit does not exist because the function approaches negative infinity (instead of a Real number) as x approaches 9 from the left. That is, x=9 is a vertical asymptote.

By the way, you can type basic math expressions with a keyboard, by using grouping smbols. The limit shown in post #9 may be typed like this:

lim[x->9] sqrt(x-3)/(x-9)

There's also a link in the forum guidelines to four pages that show how to type math. Cheers

?