Solve for A: Sin A = (sqrt(2) / 2) ; Cos A = (-sqrt (2) /2)

[jonboy]

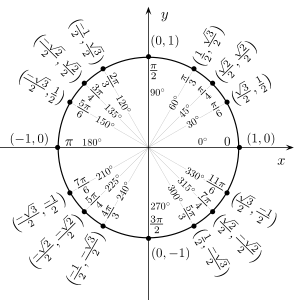
I'm teaching Trig to myself and I have this problem:

In these exercises, you are given values for Sin and Cos of A. Determine the value of A.

So I have: \(\displaystyle \L \;sin\,A\,=\,\frac{\sqrt{2}}{2}\;;\;cos\,A\,=\,\frac{\,-\,\sqrt{2}}{2}\)

I know \(\displaystyle A\) can be 45 in Sin but I don't know if that'll lead me anywhere.

 

[pka]

Because \(\displaystyle \L \frac{2}{{\sqrt 2 }} = \sqrt 2 > 1\)
there is something wrong with the problem.
Neither sine nor cosine can be greater than 1.

 

[jonboy]

Because \(\displaystyle \L \frac{2}{{\sqrt 2 }} = \sqrt 2 > 1\)
there is something wrong with the problem.
Neither sine nor cosine can be greater than 1.

I've corrected the problem but am still confused.

 

[daon]

Is "All Students Take Calculus" a familiar phrase?

For Quadrant I, All trig functions produce positive values, in II, Only Sin is positive, Tangent is positive in III, and in IV Cosine is positive. (ASTC).

Your angle has a Positive Sin value but a negative Cosine value. You also know the size if your acute reference angle. Does that help you?

 

[jonboy]

Yeah but is the acute reference angle supposed to be equal to the reference angle? If so I don't see how.

 

[Glinkx]

Yeah but is the acute reference angle supposed to be equal to the reference angle? If so I don't see how.

It often helps to imagine unit circle and to see which sign each of the functions has on that circle: