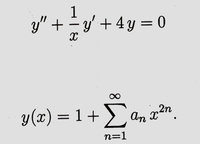Solution to Differential equation with power series

[Paul Heisenberg]

This exercise wants me to find the solution to this differential equation. Additionally they give me y(0)=1 and the requirement that y should be a even function. I should find the coefficients a1, a2, a3, a4, a5. I‘ve got my first few steps attached. The problem is that I do not understand where the 1 from the initial formula, which later should turn into a 4 (because of the distributive law), disappears. My guess is that, because they shift the index, the missing four is „kinda“ already included in the power series. The four marks there the beginning point, meaning a0 = 4. Is my guess correct, or what am I missing? Many thanks in advance.

 

[Eugenio]

That´s because [MATH]a_{0}=1[/MATH] so they do

[MATH]1 + \sum_{n=1}^{\infty }a_{n}x^{2n}=a_{0}+\sum_{n=1}^{\infty }a_{n}x^{2n}= \sum_{n=0}^{\infty }a_{n}x^{2n}[/MATH]
And then, to find [MATH]a_{1}[/MATH] the recurrence law gives, for [MATH]n=1[/MATH]
[MATH]4a_{1}+4a_{0}=0\Rightarrow 4a_{1}+4=0 \Rightarrow a_{1}=-1[/MATH]