Solid of Revolution Involving two constants

[bduncan3]

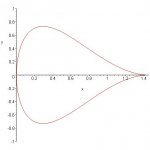
I need a little help with the following problem:

y= sqrt(x)*(x-C)^2 from 0 to C

For what value of C will the raindrop have a volume of 1? What are the approximate dimensions (length and diameter) of this shape?

I started out by expanding the equation. It makes it messy and difficult to separate. Would substitution be any help?

 

[BigGlenntheHeavy]

\(\displaystyle f(x) \ = \ x^{1/2}(x-C)^{2}\)

\(\displaystyle \mbox{Now assuming that you are revolving this function about}\)
\(\displaystyle \mbox{the }\,x\mbox{-axis (solid of revolution),one gets:}\)

\(\displaystyle V \ = \ \pi\int_{0}^{C}[x^{1/2}(x-C)^{2}]^{2}dx \ = \ \pi\int_{0}^{C}[x(x-C)^{4}]dx \ = \ 1\)

\(\displaystyle \mbox{Letting }\, x\, -\,C \, = \, u,\, du \, = \, dx, \, \mbox{and}\, x \, = \, C\,+\,u, \mbox{ we get:}\)

\(\displaystyle V \ = \ \pi\int_{-C}^{0}(C+u)u^{4}du \ = \ 1, \ = \ \pi\int_{-C}^{0}(u^{5}+Cu^{4})du \ = \ 1.\)

\(\displaystyle \mbox{Ergo, }\, V \, = \,\pi\bigg[\frac{u^{6}}{6}+\frac{Cu^{5}}{5}\bigg]_{-C}^{0} \, = \, 1 \, \mbox{ implies } \, C \, = \, \bigg(\frac{30}{\pi}\bigg)^{1/6}.\)

This is what f(x) looks like (when C = (30/Pi)^(1/6)) revolved around the x axis, with a volume of 1.

A Hershey kiss?



[attachment=0:1naugjpg]aaa.jpg[/attachment:1naugjpg]

 

[mmm4444bot]

C = (30/Pi)^(1/6)

That shape looks like a Hersheys Kiss.

(Is that due to air resistance?) :wink:

[attachment=0pk65zav]kiss1.jpg[/attachmentpk65zav]