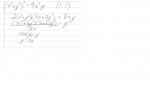slope of a line at (1,1)

[Blitze105]

i can't get this answer right... The answer is 0 and i am getting 1/2.

 

[Pklarreich]

When you diff the left side, you must get some y'-s, since you have some y-s. Try it again.

 

[pka]

\(\displaystyle \begin{gathered} \left( {x^2 + y^2 } \right)^2 = 4x^2 y \hfill \\ 2\left( {x^2 + y^2 } \right)\left[ {2x + 2yy'} \right] = 8xy + 4x^2 y' \hfill \\ \end{gathered}\)

 

[tkhunny]

Right hand side is no good. The implicit derivative needs the product rule. 4(x^2)y ==> 4[(x^2)y' + 2xy]

The left hand side needs just a little work, too.

Plus, I'm a little curious if this is the ONLY slope at (1,1). Are you sure?

 

[stapel]

In case the image doesn't display for somebody, or when it later disappears, the text in the image is as follows:

$\displaystyle \left(x^2\, +\, y^2\right)^2\, =\, 4x^2 y\, \, \left(1,\, 1\right)$

$\displaystyle 2\left(x^2\, +\, y^2\right)\left(2x\, +\, 2y\right)\, =\, 8xy'$

$\displaystyle \frac{\left(2x^2\, +\, 2y^2\right)\left(2x\, +\, 2y\right)}{8x}\, =\, y'$

$\displaystyle \frac{(4)(4)}{8}\, =\, y'$

$\displaystyle y'\, =\, \frac{1}{2}$

Notes:

The derivative of y[sup:docjiyj9]2[/sup:docjiyj9] with respect to x is not just 2y; you need to differentiate with respect to x, so there has to be a "dy/dx" in there somewhere.

The incorrect derivative of 8x[sup:docjiyj9]2[/sup:docjiyj9]y has already been pointed out, but you might want to review the Product Rule, so that you understand some of the corrections made.

Also, 16/8 is not equal to 1/2, so even if 16/8 is correct, you might want to check what follows....

Eliz.