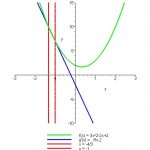
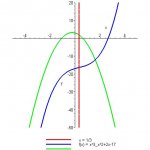
f(x)=x^3-x^2+2x-17
g(x)=-4.5x^2-2x+3
a) At what value(s) of x are the slope equations for f(x) and g(x) the same value?
my work:
x^3-x^2+2x-17=-4.5x^2-2x+3
x^3+3/5x^2+4x=20
thats as far as I have gotten
b) The concavities for f(x) and g(x) are the same value at exactly one value of x; is that common cavity up, down, or an inflection point?
g(x)=-4.5x^2-2x+3
a) At what value(s) of x are the slope equations for f(x) and g(x) the same value?
my work:
x^3-x^2+2x-17=-4.5x^2-2x+3
x^3+3/5x^2+4x=20
thats as far as I have gotten
b) The concavities for f(x) and g(x) are the same value at exactly one value of x; is that common cavity up, down, or an inflection point?