red and white kop!
Junior Member
- Joined
- Jun 15, 2009
- Messages
- 231
i am told in my book, in the middle of a domain/range section:
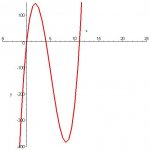
sketch the graph of x(8-2x)(22-2x)
i really have no idea of how to do this, any tips?
sketch the graph of x(8-2x)(22-2x)
i really have no idea of how to do this, any tips?