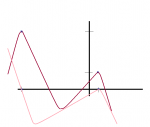
Sketch a graph of a function ...

[K_Swiss]

Sketch a graph of a function f(x) that is differentiable and that satisfies the following conditions.

$\displaystyle f'(x) > 0$, when $\displaystyle x < -5$
$\displaystyle f'(x) < 0$, when $\displaystyle -5 < x < 1$ and when $\displaystyle x > 1$
$\displaystyle f'(-5) = 0$ and $\displaystyle f'(1) = 0$
$\displaystyle f(-5) = 6$ and $\displaystyle f(1) = 2$

Did I do this question correctly, if not, please fix my mistake!

Legend:
$\displaystyle f'(x)$ is pink
$\displaystyle f(x)$ is red

 

[wjm11]

K_Swiss,

Your red graph, f(x), has a positive slope between –2 and 1, indicating that f’(x) would be positive in this region. That would conflict with the requirement that

f’(x) < 0, when –5 < x < 1.

Your red graph needs to maintain a negative slope throughout the specified region, flatten to horizontal at x = 1, then turn negative again for x > 1.