Simpson rule question

[bcddd214]

y= 1/x,[1,3]
n=4
intervals= 0,1,2,3,4

an internet video shows a method like this.
?1/3 [f(x_0 )+4f(x_1 )+2f(x_2 )+4f(x_3 )+f(x_4 ) ]
1/3 [(1/0)+4 (1/1)+2(1/2)+4 (1/3)+(1/4) ]
1/3 [4 +1+19/12]
1/3 [6 7/12]
But I go back to the text book and it is telling me to use this:
?_a^b?f(x)dx?(b-a)/6? [f(a)+4f((a+b)/2)+f(b) ]


Am I even on the right track?
I don't understand this textbook example.

 

[Deleted member 4993]

y= 1/x,[1,3]
n=4
intervals= 0,1,2,3,4

an internet video shows a method like this.
?1/3 [f(x_0 )+4f(x_1 )+2f(x_2 )+4f(x_3 )+f(x_4 ) ]
1/3 [(1/0)+4 (1/1)+2(1/2)+4 (1/3)+(1/4) ]
1/3 [4 +1+19/12]
1/3 [6 7/12]
But I go back to the text book and it is telling me to use this:
?_a^bf(x)dx ? (b-a)/6 [f(a)+4f((a+b)/2)+f(b) ]


Am I even on the right track?
I don't understand this textbook example.

That is correct Simpson's Rule

 

[bcddd214]

How do I work with that formula and do you know what it was that the other guy had me doing?

 

[mmm4444bot]

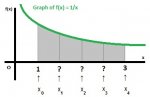
y= 1/x,[1,3]

This line (along with your subject line) tells me that they want you to approximate the area underneath the curve of y = 1/x from x = 1 through x = 3.

n=4

This line tells me that they want you to partition the given interval into four sub-intervals.

intervals= 0,1,2,3,4

I'm not sure what this line is supposed to mean. I hope those are not your x-values.



an internet video shows a method like this.

?1/3 [f(x_0 )+4f(x_1 )+2f(x_2 )+4f(x_3 )+f(x_4 ) ]

The factor 1/3 is wrong.

(b - a)/(3n) = (3 - 1)/(3)(4)

The symbolic expression inside the square brackets looks good, however.



1/3 [(1/0)+4 (1/1)+2(1/2)+4 (1/3)+(1/4) ]

Hoo boy. :roll: If your video guy divided 1 by 0, I think that you should look for a new guy. I mean, you would never write that, would you? :wink:

Well, either you did not draw a picture or you do not understand how to divide up the given interval into four pieces; otherwise, you would clearly realize that the denominators above are not 0, 1, 2, 3, and 4. The symbolic versions of the x-values (x_0, x_1, x_2, etc.) mean values on the x-axis that define the four sub-intervals (i.e., the bases of the four "rectangles").

Do you realize that you are working inside a restricted area? I mean, x never equals zero because the given interval [1, 3] does not contain the number zero. This interval does not contain the number 4, either.



1/3 [6 7/12]

This result is incorrect because the symbol f(1/0) is meaningless.



But I go back to the text book and it is telling me to use this:

?_a^b?f(x)dx?(b-a)/(3n)? [f(a)+4f((a+b)/2)+f(b) ] where n = 2

This is what Simpson's Rule would look like, were n to equal 2. Your exercise uses four subintervals, not two, so an expanded form of Simpson's Rule is needed (like you saw in your video).

Simpson's rule is based on approximating the graph by quadratic functions. It's too hard for me to explain why the expanded versions of Simpson's Rule look the way that they do, with those alternating coefficients of 4 and 2. It just divide the region up into subintervals, the same way that I would if I were using the other rules (eg: left- or right-Rieman sums, midpoint rule, trapezoid rule), and plug the x-values into the formula, without concern about what the "rectangles" look like in each case.

I guess what I'm trying to say is, "don't be too concerned if you don't fully understand why Simpson's Rule works; just understand how to apply it".

If you try again (starting with a sketch) and find that you need more help, show us what you get for the expression f(x[sub:76j8sgae]0[/sub:76j8sgae]) + 4*f(x[sub:76j8sgae]1[/sub:76j8sgae]) + 2*f(x[sub:76j8sgae]2[/sub:76j8sgae]) + 4*f(x[sub:76j8sgae]3[/sub:76j8sgae]) + f(x[sub:76j8sgae]4[/sub:76j8sgae]).


Again, those subscripted symbols for x represent the values of x (on the x-axis) at the endpoints of the four subintervals.



MY EDITS: Tried to fix my references to rectangles because Simpson's Rule is based on using a collection of arcs from quadratic functions.

 

[mmm4444bot]

Egads.

I had to come back here because I remembered that Simpson's Rule is based on parabolas, not rectangles.

I'll try to fix my post, in the morning.

I apologize for any confusion caused by my sloppiness. In the end, we still add up areas of rectangles, like you did with other methods (eg: Midpoint Rule). It's just that some of the heights are multiplied by 4 and some are multiplied by 2.

Yet, if you temporarily ignore the fact that we have parabolas as the foundation for Simpson's Rule, and think of rectangles only for the purposes of determining the x-values which break up the given interval into four subintervals, then I'm hoping that my prior post is otherwise accurate, and you'll wind up with the correct numbers for the five subscripted symbols.

Substitute those five values of x into the expanded form of Simpson's Rule for n = 4:

(b - a)/(3n) * [f(x[sub:3skjulqw]0[/sub:3skjulqw]) + 4*f(x[sub:3skjulqw]1[/sub:3skjulqw]) + 2*f(x[sub:3skjulqw]2[/sub:3skjulqw]) + 4*f(x[sub:3skjulqw]3[/sub:3skjulqw]) + f(x[sub:3skjulqw]4[/sub:3skjulqw])]

Like I said before, feel free to ask specific questions about anything that you don't understand.

 

[bcddd214]

here is what I have so far.
?1/2 [f(x_0 )+4f(x_1 )+2f(x_2 )+4f(x_3 )+f(x_4 ) ]
1/2 [(1/0)+4 (1/1)+2(1/2)+4 (1/3)+(1/4) ]
1/2 [5+19/12]
1/2 [42/12]
42/24=7/4
and that is based on your reply but,,,,
if I am supposed to be using
?_a^b?f(x)dx?(b-a)/6? [f(a)+4f((a+b)/2)+f(b) ]
I cannot see where I am applying ((a+b)/2) @??

 

[mmm4444bot]

here is what I have so far.

?1/2 [f(x_0 )+4f(x_1 )+2f(x_2 )+4f(x_3 )+f(x_4 ) ]

1/2 [(1/0)+4 (1/1)+2(1/2)+4 (1/3)+(1/4) ]

:shock:

I have totally failed you.

After I repair my ego, I will draw your sketch of the subintervals for you.

 

[bcddd214]

My friend, you are already being soooo helpful. In no way have you failed me.
I am deeply in your debt.

 

[mmm4444bot]

I'm disappointed that you are still trying to divide by zero. Division by zero is not allowed, in the Real number system, because it is meaningless. Hence, the fraction 1/0 is nonsense.

I'm disappointed that you are still using the x-values of 0, 1, 2, 3, and 4 in your f(x) calculations. I tried to tell you that's wrong. We cannot have 0 and 4, for example, to calculate f(0) and f(4), because we are working only with x values from 1 through 3. That is the restricted interval [1, 3].

You told me that your latest work is "based on my reply", so my reply must not be clear to you. (I'm now working on a diagram to upload for you, but the computer owner needs his machine, too, so it will be awhile.)

 

[mmm4444bot]

Here is my sketch of the graph of y = f(x) showing the area underneath the curve from x = 1 through x = 3. It is this shaded area that we are trying to approximate using Simpson's Rule.

They told you that n = 4. This means that they want the region to be split into four pieces.

Hence, the interval [1, 3] is divided into four subintervals of EQUAL width.

The width of each subinterval is (b - a)/n.



The values of x that define these four subintervals are labeled 1 - ? - ? - ? - 3.

The SAME values of x are also represented by the symbols x[sub:1q2n6qxp]0[/sub:1q2n6qxp] - x[sub:1q2n6qxp]1[/sub:1q2n6qxp] - x[sub:1q2n6qxp]2[/sub:1q2n6qxp] - x[sub:1q2n6qxp]3[/sub:1q2n6qxp] - x[sub:1q2n6qxp]4[/sub:1q2n6qxp], as shown.

Hence, we see right away that x[sub:1q2n6qxp]0[/sub:1q2n6qxp] = 1 and x[sub:1q2n6qxp]4[/sub:1q2n6qxp] = 3.



[attachment=0:1q2n6qxp]four intervals.jpg[/attachment:1q2n6qxp]

You need to calculate the remaining three values of x (shown with ? marks). For example, what is the value of x halfway between 1 and 3? That number is x[sub:1q2n6qxp]2[/sub:1q2n6qxp].

Use that number to calculate the value of x halfway between x[sub:1q2n6qxp]0[/sub:1q2n6qxp] and x[sub:1q2n6qxp]2[/sub:1q2n6qxp]. That's x[sub:1q2n6qxp]1[/sub:1q2n6qxp].

Finally, what is the number halfway between x[sub:1q2n6qxp]2[/sub:1q2n6qxp] and x[sub:1q2n6qxp]4[/sub:1q2n6qxp]? That's x[sub:1q2n6qxp]3[/sub:1q2n6qxp].


Once you have the correct numbers for the symbols x[sub:1q2n6qxp]0[/sub:1q2n6qxp], x[sub:1q2n6qxp]1[/sub:1q2n6qxp], x[sub:1q2n6qxp]2[/sub:1q2n6qxp], x[sub:1q2n6qxp]3[/sub:1q2n6qxp], and x[sub:1q2n6qxp]4[/sub:1q2n6qxp], substitute them (along with your other values for symbols a, b, and n) into the expanded formula for Simpson's Rule:

(b - a)/(3n) * [f(x[sub:1q2n6qxp]0[/sub:1q2n6qxp]) + 4*f(x[sub:1q2n6qxp]1[/sub:1q2n6qxp]) + 2*f(x[sub:1q2n6qxp]2[/sub:1q2n6qxp]) + 4*f(x[sub:1q2n6qxp]3[/sub:1q2n6qxp]) + f(x[sub:1q2n6qxp]4[/sub:1q2n6qxp])]

I still think that you should get 11/10.