Simplifying Logarithmic Function y=14log2(8x−56)16−12 by applying log properties
Hello, here is the exact problem that I am struggling with:
Simplify the equation [FONT=MathJax_Math]y[/FONT][FONT=MathJax_Main]=[/FONT][FONT=MathJax_Main]1[/FONT][FONT=MathJax_Main]4[/FONT][FONT=MathJax_Main]log[/FONT][FONT=MathJax_Main]2[/FONT][FONT=MathJax_Main]([/FONT][FONT=MathJax_Main]8[/FONT][FONT=MathJax_Math]x[/FONT][FONT=MathJax_Main]−[/FONT][FONT=MathJax_Main]56[/FONT][FONT=MathJax_Main])[/FONT][FONT=MathJax_Main]16[/FONT][FONT=MathJax_Main]−[/FONT][FONT=MathJax_Main]12[/FONT]by applying the laws of logarithms. How are the original equation and the simplified equation related?
I have had no problems simplifying logarithmic expressions before when I am solving for an unknown variable.
The issue here appears to be that I don't recognize any of the laws for logarithms at work that I can reverse that wouldn't fundamentally change the function. The simplified version has to be equivalent to the original.
I have tried many different angles, such as transforming it to exponential form, but none of them have worked for me.
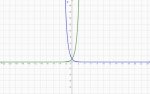
I put the question into WolframAlpha, but when I put the answer it gave me into graphing software, the simplified version and the original did not map onto each other.
Thank you for any help that you can provide. [FONT=MathJax_Math]y[/FONT][FONT=MathJax_Main]=[/FONT][FONT=MathJax_Main]1[/FONT][FONT=MathJax_Main]4[/FONT][FONT=MathJax_Main]log[/FONT][FONT=MathJax_Main]2[/FONT][FONT=MathJax_Main]([/FONT][FONT=MathJax_Main]8[/FONT][FONT=MathJax_Math]x[/FONT][FONT=MathJax_Main]−[/FONT][FONT=MathJax_Main]56[/FONT][FONT=MathJax_Main])[/FONT][FONT=MathJax_Main]16[/FONT]
Hello, here is the exact problem that I am struggling with:
Simplify the equation [FONT=MathJax_Math]y[/FONT][FONT=MathJax_Main]=[/FONT][FONT=MathJax_Main]1[/FONT][FONT=MathJax_Main]4[/FONT][FONT=MathJax_Main]log[/FONT][FONT=MathJax_Main]2[/FONT][FONT=MathJax_Main]([/FONT][FONT=MathJax_Main]8[/FONT][FONT=MathJax_Math]x[/FONT][FONT=MathJax_Main]−[/FONT][FONT=MathJax_Main]56[/FONT][FONT=MathJax_Main])[/FONT][FONT=MathJax_Main]16[/FONT][FONT=MathJax_Main]−[/FONT][FONT=MathJax_Main]12[/FONT]by applying the laws of logarithms. How are the original equation and the simplified equation related?
I have had no problems simplifying logarithmic expressions before when I am solving for an unknown variable.
The issue here appears to be that I don't recognize any of the laws for logarithms at work that I can reverse that wouldn't fundamentally change the function. The simplified version has to be equivalent to the original.
I have tried many different angles, such as transforming it to exponential form, but none of them have worked for me.
I put the question into WolframAlpha, but when I put the answer it gave me into graphing software, the simplified version and the original did not map onto each other.
Thank you for any help that you can provide. [FONT=MathJax_Math]y[/FONT][FONT=MathJax_Main]=[/FONT][FONT=MathJax_Main]1[/FONT][FONT=MathJax_Main]4[/FONT][FONT=MathJax_Main]log[/FONT][FONT=MathJax_Main]2[/FONT][FONT=MathJax_Main]([/FONT][FONT=MathJax_Main]8[/FONT][FONT=MathJax_Math]x[/FONT][FONT=MathJax_Main]−[/FONT][FONT=MathJax_Main]56[/FONT][FONT=MathJax_Main])[/FONT][FONT=MathJax_Main]16[/FONT]