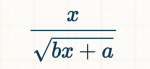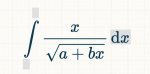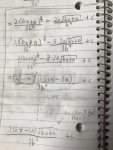flyingfishcattle
New member
- Joined
- Dec 25, 2018
- Messages
- 1
Hi,
I have evaluated the integral for:
. . . . .\(\displaystyle \displaystyle \int\, \dfrac{x}{\sqrt{a\, +\, bx\,}}\, dx\)
For my answer I got:
. . . . .\(\displaystyle \displaystyle \dfrac{2\, (bx\, +\, a)^{3/2}}{3b^2}\, -\, \dfrac{2a\, \sqrt{bx\, +\, a\,}}{b^2}\, +\, C\)
But I don't know how to simplify that above to get the below:
. . . . .\(\displaystyle \displaystyle \dfrac{2\, (bx\, -\, 2a)\, \sqrt{bx\, +\, a\,}}{3b^2}\, +\, C\)
Here is my work so far:
. . . . .\(\displaystyle \begin{align}\displaystyle \dfrac{2\, (bx\, +\, a)^{3/2}}{3b^2}\, -\, \dfrac{2a\, \sqrt{bx\, +\, a\,}}{b^2}\, +\, C\, &=\, \dfrac{2\, (bx\, +\, a)^{3/2}}{3b^2}\, -\, \dfrac{3\, \cdot\, 2a\, \sqrt{bx\, +\, a\,}}{3\, \cdot\, b^2}\, +\, C\\
\\
&=\, \dfrac{2\, (bx\, +\, a)^{3/2}\, -\, 3\, \cdot\, 2a\, \sqrt{bx\, +\, a\,}}{3b^2}\\
\\
&=\, \dfrac{\left(2\, \sqrt{bx\, +\, a\,}\right)\, \big((bx\, +\, a)\, -\, 3a\big)}{3b^2}\end{align}\)
How do I get from this to the final form, below?
. . . . .\(\displaystyle \displaystyle \dfrac{2\, (bx\, -\, 2a)\, \sqrt{bx\, +\, a\,}}{3b^2}\, +\, C\)
Any help would be appreciated
I have evaluated the integral for:
. . . . .\(\displaystyle \displaystyle \int\, \dfrac{x}{\sqrt{a\, +\, bx\,}}\, dx\)
For my answer I got:
. . . . .\(\displaystyle \displaystyle \dfrac{2\, (bx\, +\, a)^{3/2}}{3b^2}\, -\, \dfrac{2a\, \sqrt{bx\, +\, a\,}}{b^2}\, +\, C\)
But I don't know how to simplify that above to get the below:
. . . . .\(\displaystyle \displaystyle \dfrac{2\, (bx\, -\, 2a)\, \sqrt{bx\, +\, a\,}}{3b^2}\, +\, C\)
Here is my work so far:
. . . . .\(\displaystyle \begin{align}\displaystyle \dfrac{2\, (bx\, +\, a)^{3/2}}{3b^2}\, -\, \dfrac{2a\, \sqrt{bx\, +\, a\,}}{b^2}\, +\, C\, &=\, \dfrac{2\, (bx\, +\, a)^{3/2}}{3b^2}\, -\, \dfrac{3\, \cdot\, 2a\, \sqrt{bx\, +\, a\,}}{3\, \cdot\, b^2}\, +\, C\\
\\
&=\, \dfrac{2\, (bx\, +\, a)^{3/2}\, -\, 3\, \cdot\, 2a\, \sqrt{bx\, +\, a\,}}{3b^2}\\
\\
&=\, \dfrac{\left(2\, \sqrt{bx\, +\, a\,}\right)\, \big((bx\, +\, a)\, -\, 3a\big)}{3b^2}\end{align}\)
How do I get from this to the final form, below?
. . . . .\(\displaystyle \displaystyle \dfrac{2\, (bx\, -\, 2a)\, \sqrt{bx\, +\, a\,}}{3b^2}\, +\, C\)
Any help would be appreciated
Attachments
Last edited by a moderator: