Simplifying fractions with a decimal

[fractions91a]

Good afternoon,

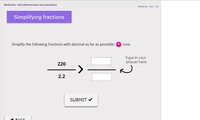
I am having some trouble with finding the correct answer for the following fraction (please see attached photo).

I thought the answer would be 22 / .22, however this is incorrect. If anyone can help me reach the correct answer, I would be very greatful.

Thank you kindly.

 

[Gnomeland]

Hello!

The way that I would go about solving this question is first getting rid of any decimals in the fraction. Decimals shouldn't be in fractions ever, at least in math class, and especially for a final answer.

In this case, you can multiply both the top (numerator) and bottom (denominator) by 10, giving you 2200/22

Then you can simply divide the top and bottom by the greatest common factor like usual (22) and get your answer, 100/1 or just 100

Feel free to ask any follow up questions that you have!

 

[topsquark]

Is it possible they are looking for 2200/22?

-Dan

 

[Otis]

Is it possible they are looking for 2200/22?

I'm thinking "simplify as much as possible" means "reduce the ratio as much as possible", so I'd try 100/1.

I'm thinking the greater-than symbol > between the given and reduced ratios was used to mean something like "becomes" or "reduces to". That's a very poor choice of symbols.

 

[fractions91a]

I'm thinking "simplify as much as possible" means "reduce the ratio as much as possible", so I'd try 100/1.

I'm thinking the greater-than symbol > between the given and reduced ratios was used to mean something like "becomes" or "reduces to". Very poor choice of symbols.

Thank you kindly! This was the correct answer.

 

[Otis]

… I thought the answer would be 22 / .22, however this is incorrect …

Hi fractions. The ratios 22/0.22 and 220/2.2 are equal, but the exercise seems to want the ratio reduced. That means cancelling common factors. Let's look at the rational form of 2.2 (which is 22/10) and see how the given numerator and denominator can reduce.

\[\frac{220}{2.2} = \frac{220}{\frac{22}{10}}\]

We rarely divide by fractions. Instead of dividing 220 by 22/10, we multiply 220 by the reciprocal of 22/10, instead. That's a general rule. (The reciprocal of 22/10 is 10/22.)

\[\frac{220}{\frac{22}{10}} = \frac{220}{1} × \frac{10}{22}\]

Hopefully you realize that 220 and 22 share a common factor of 22. It cancels. (If you're not sure why, let us know.)

\[\frac{\cancel{220}^{10}}{1} × \frac{10}{\cancel{22}_1} = \frac{10 × 10}{1 × 1} = \frac{100}{1}\]

?