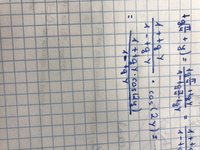Simplify the Phenomenon

[naomiik]

Hi, I need your help with simplifying this phenomenon.

 

[Dr.Peterson]

I would call that an expression, not a phenomenon ...

Apply the angle-sum formula for the tangent. Then see what else you can do. At some point you will likely be expressing tangents in terms of sine and cosine.

Please show what you have tried, if you need more help, because that's how we work here.

 

[Deleted member 4993]

Hi, I need your help with simplifying this phenomenon. View attachment 22934

Use the fact:

tan(A+B) = [tan(A) + tan(B)]/[1 - tan(A) * tan(B)]​

Please show us what you have tried and exactly where you are stuck.

Please follow the rules of posting in this forum, as enunciated at:

READ BEFORE POSTING​

Please share your work/thoughts about these problems.

 

[naomiik]

These are previous exercises that I did correctly:

In my textbook it’s written that I have to simplify the phenomenon so idk ??‍
-
Where I’m stuck is shown in second picture. I applied formulas that are given in textbook but I’m not sure what to do now.

 

[Dr.Peterson]

Where I’m stuck is shown in second picture. I applied formulas that are given in textbook but I’m not sure what to do now.

Don't use the double-angle formula, as that results in functions of two different angles. Instead, do as I hinted, and write the tangents as sine/cosine, and simplify algebraically.

 

[naomiik]

Don't use the double-angle formula, as that results in functions of two different angles. Instead, do as I hinted, and write the tangents as sine/cosine, and simplify algebraically.

So instead of cos(2y) I should write 1-2sin^2(y) or just leave like in the given expression?
I have no idea how to write tangents as sine/cosine:/

 

[Deleted member 4993]

So instead of cos(2y) I should write 1-2sin^2(y) or just leave like in the given expression?
I have no idea how to write tangents as sine/cosine:/

Are you saying that you do not know:

tan(Θ) = sin(Θ)/cos(Θ)

 

[Dr.Peterson]

So instead of cos(2y) I should write 1-2sin^2(y) or just leave like in the given expression?
I have no idea how to write tangents as sine/cosine:/

Leave [MATH]\cos^2(\gamma)-\sin^2(\gamma)[/MATH] as it is. The given form will work out nicely.

A standard technique for simplifying a trig expression when you see nothing else to do is to express all functions in terms of sine and cosine. Surely you have seen the reciprocal and quotient identities.