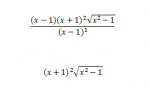Simplify and remove fractional exponent problem - driving me nuts! Please help!

[han_bozo]

Can anyone help me with the following? I've hit a major wall with this and am feeling very deflated

Need to simplify whilst removing all fractional exponents.

(X2-1)² x (X+1)^1/2 divided by (x-1)^3/2

 

[stapel]

Need to simplify whilst removing all fractional exponents.

(X2-1)² x (X+1)^1/2 divided by (x-1)^3/2

I will guess that the first lower-case "x" is meant to be "times", while the second lower-case "x" is meant to be the variable "X", so the expression is as follows:

. . . . .\(\displaystyle \dfrac{(x^2\, -\, 1)^2\, (x\, +\, 1)^{\frac{1}{2}}}{(x\, -\, 1)^{\frac{3}{2}}}\)

Is the above correct? If not, please reply with corrections. If so, then the first step (since you're supposed to get rid of the fractional parts of the powers) is to convert to radical notation (here):

. . . . .\(\displaystyle \dfrac{(x^2\, -\, 1)^2\, \sqrt{\strut x\, +\, 1\, }}{\sqrt{\strut (x\, -\, 1)^3\,}}\)

Then start simplifying, and also rationalizing the denominator (here):

. . . . .\(\displaystyle \dfrac{(x\, -\, 1)^2\, (x\, +\, 1)^2\, \sqrt{\strut x\, +\, 1\,}}{(x\, -\, 1)\, \sqrt{\strut x\, -\, 1\, }}\, =\, \dfrac{(x\, -\, 1)\, (x\, +\, 1)^2\, \sqrt{\strut x\, +\, 1\, }}{\sqrt{\strut x\, -\, 1\, }}\, =\, \dfrac{(x\, -\, 1)\, (x\, +\, 1)^2\, \sqrt{\strut x\, +\, 1\, }\, \sqrt{\strut x\, -\, 1\,}}{\sqrt{\strut x\, -\, 1\, }\, \sqrt{\strut x\, -\, 1\,}}\)

...and so forth.

I've hit a major wall with this....

How far did you get? Please reply showing your progress so far. Thank you! :wink:

 

[han_bozo]

Sorry, I'm a bit new to writing mathematical expressions online (maybe there is a guide somewhere?).

Anyway, you Sir, are an absolute Godsend!!!! That's some really smart manipulation of some of the terms there!! I've basically finished off am left with the bottom bit which is definitely right!!

Never ceases to amaze me just how 'creative' you guys are at finding solutions to problems.... I hope it's something I can acquire with determination and lots of practice!!! Thank you so much again!!

btw: i deliberately showed (x-1) to the power of 1 to indicate that the '1/2' powers summed to 1 for anyone who had a similar problem.

 

[stapel]

Anyway, you Sir, are an absolute Godsend! That's some really smart manipulation of some of the terms there!

Never ceases to amaze me just how 'creative' you guys are at finding solutions to problems.... I hope it's something I can acquire with determination and lots of practice!

*blush* You are too kind!

But you're quite right about the "practice" part, because that's how we get so "smart": we've been around this block many, many times, so we've seen some of these tricks enough that we've remembered them. And that's a good take-away for you: remember this kind of manipulation, because it'll probably prove very helpful on the next test.