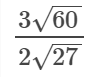Simplify (3\sqrt(60))/(2\sqrt(27))

[Grimsuke]

\(\displaystyle \large{ \dfrac{3\, \sqrt{\strut 60\,}}{2\, \sqrt{\strut 27\,}}}\)

For this equation, I have to simplify it, although I'm not sure how to start.
I haven't done any previous attempts to solve it yet.

 

[ksdhart2]

A good place to start to is recall one of the basic rules of square roots that you learned: \(\displaystyle \sqrt{a \cdot b}=\sqrt{a} \cdot \sqrt{b}\). Looking just at the numerator, 60 has a lot of factors. Can you think of any where pulling it out would simplify things? Now, looking just at the denominator, 27 doesn't have as many factors, but does it have any "nice" factors? After doing this factoring, what are you left with? Where do you think you might go from there?

 

[stapel]

\(\displaystyle \large{ \dfrac{3\, \sqrt{\strut 60\,}}{2\, \sqrt{\strut 27\,}}}\)

For this [expression], I have to simplify it, although I'm not sure how to start.

To learn how to work with square roots, try any of the lessons listed here.

 

[Deleted member 4993]

\(\displaystyle \large{ \dfrac{3\, \sqrt{\strut 60\,}}{2\, \sqrt{\strut 27\,}}}\)

For this equation, I have to simplify it, although I'm not sure how to start.
I haven't done any previous attempts to solve it yet.

60 = 4 * 15 and 27 = 9 * 3

What does that tell you?

 

[pka]

\(\displaystyle \large{ \dfrac{3\, \sqrt{\strut 60\,}}{2\, \sqrt{\strut 27\,}}}\).

You simpliy do not understand what this is about.
\(\displaystyle 60=2^2(3)(5)\)