Simple problem from calc homework

[justin984]

[Removed]

 

[Deleted member 4993]

Hi, sorry if this question is pretty basic. Im in my first few weeks of calculus 1. The homework is already submitted fyi.

Here is the problem:
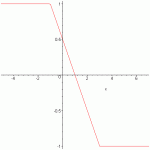
Find the constants a and b such that the function is continuous on the entire real line.

f(x) = 1, if x<= -1
f(x) = ax+b, if -1<x<3
f(x) = -1, if x>= 3

And here is what I tried:
lim (x->-1+) = -a+b = 1

lim (x->3-) = 3a + b = -1

-a + b = 1
(+) 3a + b = -1
------------------------
2a + 2b = 0
2(a + b) = 0
a +b = 0

I'm not sure what to do from here. Any help is much appreciated!

You have two equations and two unknowns - solve it! This is algebra - you are in calculus......

- a + b = 1........................(1)
3a + b = -1........................(2)

subtract (1) from (2)

4a = -2

a = - 1/2

now continue....

 

[justin984]

[Removed]

 

[stapel]

Thank you for your help. Howcome you subtracted them?

To cancel out the one variable.

To learn how to solve systems of linear equations, try here. After studying the lesson, the solution you were provided should make a lot more sense. :wink:

 

[BigGlenntheHeavy]

[attachment=0:ykiufubl]Piece.gif[/attachment:ykiufubl]

Now, find the equation of the oblique line.

Hint: You know two points on the line (-1,1) and(3,-1)