simple algebra at the end of a calc problem
- Thread starter CalcGuy
- Start date
Hello, CalcGuy!
I see nothing wrong with your answer.
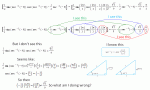
\(\displaystyle \text{We have: }\:\frac{1}{2}\cdot\sin\left[\sec^{-1}(-9)\right]\cdot\cos\left[\sec^{-1}(-9)\right]\)
\(\displaystyle \text{Let: }\:\theta \,=\,\sec^{-1}(-9) \quad\Rightarrow\quad \sec\theta \:=\:\frac{9}{-1} \:=\:\frac{hyp}{adj}\)
\(\displaystyle \text{So, }\theta\text{ is in a right triangle with: }\:adj = -1,\;hyp = 9\)
\(\displaystyle \text{Assuming }\theta\text{ is in Quadrant 3, we have: }\
pp \,=\,-\sqrt{80}\,=\,-4\sqrt{5}\)
\(\displaystyle \text{Hence: }\:\sin\theta \:=\:-\frac{4\sqrt{5}}{9},\;\;\cos\theta \:=\:-\frac{1}{9}\)
\(\displaystyle \text{Therefore: }\:\frac{1}{2}\sin\theta\cos\theta \;=\;\frac{1}{2}\left(-\frac{4\sqrt{5}}{9}\right)\left(-\frac{1}{9}\right) \;=\;\frac{2\sqrt{5}}{81}\)
I see nothing wrong with your answer.
\(\displaystyle \text{We have: }\:\frac{1}{2}\cdot\sin\left[\sec^{-1}(-9)\right]\cdot\cos\left[\sec^{-1}(-9)\right]\)
\(\displaystyle \text{Let: }\:\theta \,=\,\sec^{-1}(-9) \quad\Rightarrow\quad \sec\theta \:=\:\frac{9}{-1} \:=\:\frac{hyp}{adj}\)
\(\displaystyle \text{So, }\theta\text{ is in a right triangle with: }\:adj = -1,\;hyp = 9\)
\(\displaystyle \text{Assuming }\theta\text{ is in Quadrant 3, we have: }\
pp \,=\,-\sqrt{80}\,=\,-4\sqrt{5}\)\(\displaystyle \text{Hence: }\:\sin\theta \:=\:-\frac{4\sqrt{5}}{9},\;\;\cos\theta \:=\:-\frac{1}{9}\)
\(\displaystyle \text{Therefore: }\:\frac{1}{2}\sin\theta\cos\theta \;=\;\frac{1}{2}\left(-\frac{4\sqrt{5}}{9}\right)\left(-\frac{1}{9}\right) \;=\;\frac{2\sqrt{5}}{81}\)
BigGlenntheHeavy
Senior Member
- Joined
- Mar 8, 2009
- Messages
- 1,577
\(\displaystyle Note: \ arcsec(-9) \ = \ arcsin(1/9)+\pi/2\)
\(\displaystyle Also \ note: \ \int_{-2}^{-9}\frac{\sqrt{x^{2}-1}}{x^{3}}dx \ = \ -\int_{-9}^{-2}\frac{\sqrt{x^{2}-1}}{x^{3}}dx\)
\(\displaystyle Is \ your \ Professor \ a \ trickster?\)
\(\displaystyle Hence, \ final \ solution \ = \ (1/2)[t-sin(t)cos(t)]_{arcsin(1/9)+\pi/2}^{2\pi/3}\)
\(\displaystyle = \ \frac{1}{2}\bigg[\frac{2\pi}{3}-(\frac{\sqrt3}{2})(\frac{-1}{2})-[arcsin(1/9)+\frac{\pi}{2}-(\frac{4\sqrt5}{9})(\frac{-1}{9})]\bigg]\)
\(\displaystyle = \ \frac{1}{2}\bigg[\frac{2\pi}{3}+\frac{\sqrt3}{4}-arcsin(1/9)-\frac{\pi}{2}-\frac{4\sqrt5}{81}\bigg] \ = \ about \ .367424\)
\(\displaystyle Also \ note: \ \int_{-2}^{-9}\frac{\sqrt{x^{2}-1}}{x^{3}}dx \ = \ -\int_{-9}^{-2}\frac{\sqrt{x^{2}-1}}{x^{3}}dx\)
\(\displaystyle Is \ your \ Professor \ a \ trickster?\)
\(\displaystyle Hence, \ final \ solution \ = \ (1/2)[t-sin(t)cos(t)]_{arcsin(1/9)+\pi/2}^{2\pi/3}\)
\(\displaystyle = \ \frac{1}{2}\bigg[\frac{2\pi}{3}-(\frac{\sqrt3}{2})(\frac{-1}{2})-[arcsin(1/9)+\frac{\pi}{2}-(\frac{4\sqrt5}{9})(\frac{-1}{9})]\bigg]\)
\(\displaystyle = \ \frac{1}{2}\bigg[\frac{2\pi}{3}+\frac{\sqrt3}{4}-arcsin(1/9)-\frac{\pi}{2}-\frac{4\sqrt5}{81}\bigg] \ = \ about \ .367424\)
mmm4444bot
Super Moderator
- Joined
- Oct 6, 2005
- Messages
- 10,962
When I evaluate the given equation, I don't get equality.
0.3674 ? 0.2381
0.3674 ? 0.2381
BigGlenntheHeavy
Senior Member
- Joined
- Mar 8, 2009
- Messages
- 1,577
\(\displaystyle Note: \ For \ what \ it \ is \ worth \ dept., \ just \ my \ opinion.\)
\(\displaystyle When \ working \ with \ trig. \ functions, \ I \ always \ (if \ possible) \ try \ to \ break \ them \ down \ into \ sin, \ cos,\)
\(\displaystyle \ or \ tan \ functions \ and \ also \ get \ rid \ of \ any \ negative \ signs, \ if \ possible; \ as \ this \ will \ make \ it\)
\(\displaystyle \ easier, \ I \ have \ found \ to \ solve.\)
\(\displaystyle For \ example: \ sec(t) \ = \ -9, \ \frac{1}{cos(t)} \ = \ -9, \ cos(t) \ = \ \frac{-1}{9}\)
\(\displaystyle sin(\frac{\pi}{2}-t) \ = \ \frac{-1}{9}, \ \frac{\pi}{2}-t \ = \ arcsin(\frac{-1}{9})\)
\(\displaystyle t \ = \ \frac{\pi}{2}-arcsin(\frac{-1}{9}) \ = \ \frac{\pi}{2}+arcsin(\frac{1}{9})\)
\(\displaystyle Last \ one: \ Let \ k \ = \ -arcsin(\frac{-1}{9}), \ then \ -k \ = \ arcsin(\frac{-1}{9})\)
\(\displaystyle Hence, \ sin(-k) \ = \ (\frac{-1}{9}), \ -sin(k) \ = \ (\frac{-1}{9}), \ \implies \ sin(k) \ = \ \frac{1}{9}, \ k \ = \ arcsin(1/9)\)
\(\displaystyle Therefore, \ -arcsin(\frac{-1}{9}) \ = \ k \ = \ arcsin(\frac{1}{9})\)
\(\displaystyle All \ this \ grunt \ work \ could \ have \ been \ avoided, \ by \ just \ punching \ in \ arccos(1/-9) \ into \ your\)
\(\displaystyle \ trusty \ TI-89 \ and \ you \ would \ have \ gotten \ \ arcsin(1/9) \ + \ \pi/2.\)
\(\displaystyle The \ TI-89 \ tells \ no \ lies, \ the \ TI-89 \ knows \ best.\)
\(\displaystyle When \ working \ with \ trig. \ functions, \ I \ always \ (if \ possible) \ try \ to \ break \ them \ down \ into \ sin, \ cos,\)
\(\displaystyle \ or \ tan \ functions \ and \ also \ get \ rid \ of \ any \ negative \ signs, \ if \ possible; \ as \ this \ will \ make \ it\)
\(\displaystyle \ easier, \ I \ have \ found \ to \ solve.\)
\(\displaystyle For \ example: \ sec(t) \ = \ -9, \ \frac{1}{cos(t)} \ = \ -9, \ cos(t) \ = \ \frac{-1}{9}\)
\(\displaystyle sin(\frac{\pi}{2}-t) \ = \ \frac{-1}{9}, \ \frac{\pi}{2}-t \ = \ arcsin(\frac{-1}{9})\)
\(\displaystyle t \ = \ \frac{\pi}{2}-arcsin(\frac{-1}{9}) \ = \ \frac{\pi}{2}+arcsin(\frac{1}{9})\)
\(\displaystyle Last \ one: \ Let \ k \ = \ -arcsin(\frac{-1}{9}), \ then \ -k \ = \ arcsin(\frac{-1}{9})\)
\(\displaystyle Hence, \ sin(-k) \ = \ (\frac{-1}{9}), \ -sin(k) \ = \ (\frac{-1}{9}), \ \implies \ sin(k) \ = \ \frac{1}{9}, \ k \ = \ arcsin(1/9)\)
\(\displaystyle Therefore, \ -arcsin(\frac{-1}{9}) \ = \ k \ = \ arcsin(\frac{1}{9})\)
\(\displaystyle All \ this \ grunt \ work \ could \ have \ been \ avoided, \ by \ just \ punching \ in \ arccos(1/-9) \ into \ your\)
\(\displaystyle \ trusty \ TI-89 \ and \ you \ would \ have \ gotten \ \ arcsin(1/9) \ + \ \pi/2.\)
\(\displaystyle The \ TI-89 \ tells \ no \ lies, \ the \ TI-89 \ knows \ best.\)