jake.bradley
New member
- Joined
- Apr 30, 2010
- Messages
- 3
Use the Shell Method to compute the volume of the solids obtained by rotating the region enclosed by the graphs of the functions y=x^2, y=8-x^2 and x=1 about the y-axis.
AND
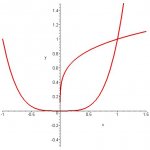
Shell Method to computer volume obtained by rotating the region enclosed by functions y=x^4 and y=x^(1/4) about the y-axis.
No idea where to start, please please help.
AND
Shell Method to computer volume obtained by rotating the region enclosed by functions y=x^4 and y=x^(1/4) about the y-axis.
No idea where to start, please please help.