Undeadpaladin
New member
- Joined
- Feb 19, 2008
- Messages
- 1
I'm not totally sure how to set up this intergral using the shell method. I don't have to solve for it(That's the easy part, go figure!). My problem is typically when revolving the object about a line not the axis i have some trouble.
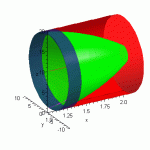
The problem is as follows :
y = x^3
y = 1
x = 2
use the shell method about the line y = 10
My fire time posting i'm not sure exactly how to use symbols, but i came up with this
2Pi * Intergral bottom limit = 2, top limit = 8
[ (10-y)(2-y^(1/3) ] dy
The limits for intergration should be right i think, it's the second part i can't seem to figure out exactly. Any help would be welcome!
The problem is as follows :
y = x^3
y = 1
x = 2
use the shell method about the line y = 10
My fire time posting i'm not sure exactly how to use symbols, but i came up with this
2Pi * Intergral bottom limit = 2, top limit = 8
[ (10-y)(2-y^(1/3) ] dy
The limits for intergration should be right i think, it's the second part i can't seem to figure out exactly. Any help would be welcome!