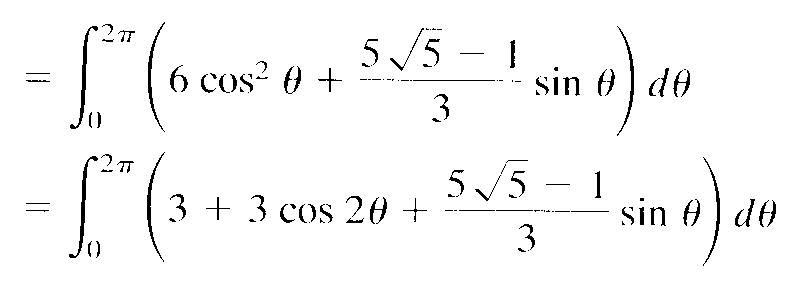G
Guest
Guest
Hi can someone help me with the fatorial and prove why is it zero? I don't understand it and thus I can't apply it to other factorials in my calculus problems to see if it's divergent or convergent such as 1/(n+1)!
\(\displaystyle \sum_{n=1}^\infty \frac{1}{n!}\)
Thanks.
And also, I don't quite understand this. Can someone please explain it to me word for word that is understandable, preferiably in laymen's term. Thanks.
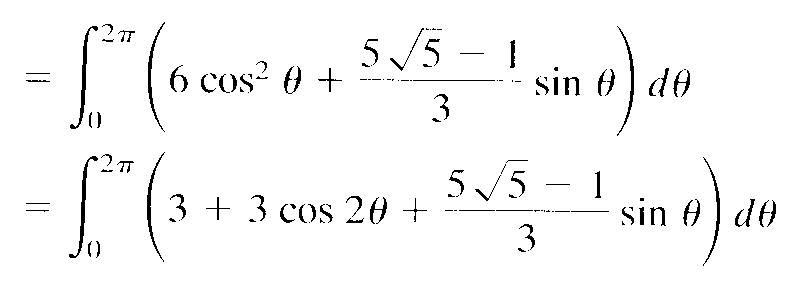
\(\displaystyle \sum_{n=1}^\infty \frac{1}{n!}\)
Thanks.
And also, I don't quite understand this. Can someone please explain it to me word for word that is understandable, preferiably in laymen's term. Thanks.