Hello!
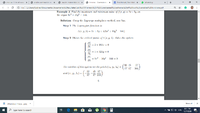
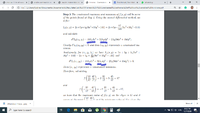
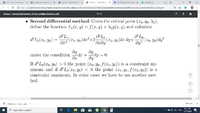
Trying to solve a problem that requested to find the extrema with constraints of a function, after constructing the Lagrangian function and differentiating and all of that, I've seen that in the second differential method for establishing if one critical point is a maximum or a minimum, the therm that contains dx*dy disappears, while the ones with dx^2 and dy^2 are always taken into consideration. I was wondering why the therm with dx*dy disappears?
I've attached a picture with the theory and 2 pictures with an example.
Thank you so much!
Trying to solve a problem that requested to find the extrema with constraints of a function, after constructing the Lagrangian function and differentiating and all of that, I've seen that in the second differential method for establishing if one critical point is a maximum or a minimum, the therm that contains dx*dy disappears, while the ones with dx^2 and dy^2 are always taken into consideration. I was wondering why the therm with dx*dy disappears?
I've attached a picture with the theory and 2 pictures with an example.
Thank you so much!