owningbro2
New member
- Joined
- Sep 9, 2008
- Messages
- 11
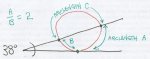
A secant and a tangent to a circle intersect to form an angle of 38 degrees. IF the measures of the arcs intercepted by this angle are in a ratio of 2:1 find the measure of the third arc.
I have no clue to solving this problem.
I did try to do the problem but it led me to nowhere.
Thank you for your help....
I have no clue to solving this problem.
I did try to do the problem but it led me to nowhere.
Thank you for your help....