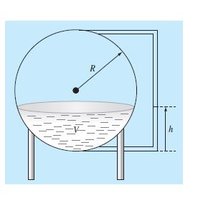
You are given that when the depth of the water is "h" the volume of water is \(\displaystyle V= \frac{\pi R^2(3R- h)}{3}\). With R= 3 m, that is \(\displaystyle V= \(\displaystyle V= 3\pi(9- h)\) You want to determine what h is when V= 30 so you want to solve \(\displaystyle \frac{9\pi (9- h)}{3}= 3\pi(9- h)= 30\). Taking \(\displaystyle \pi\) to be 3.14, that is \(\displaystyle 9.42(9- h)= 30\). ( Solving that numerically seems silly since this is a linear equation in h and it is easy to solve for \(\displaystyle h= 5.81\) but I guess this is for practice.)
The "secant method" solves the equation f(h)= a by starting with two values for h, say \(\displaystyle h_1\) and \(\displaystyle h_2\), such that one of \(\displaystyle f(x_1)\) and \(\displaystyle f(x_2)\) is greater than a and the other less, calculating the equation of the line \(\displaystyle y= ah+ b\) between the two points and solving \(\displaystyle ah+ b= 0\) to get a point hopefully closer to the root than the previous two. If that new point satisfies f(h)= 0 we are done. If not, it is either positive of negative. We choose the one of \(\displaystyle x_1\) and \(\displaystyle x_2\) that gives the other sign and repeat.
Here for example we might take h= 1 to get V= 75.36 > 30 and h= 10 to get V= -9.42< 30. The straight line between (1, 75.36) and (10, -9.42) has slope (-9.42- 75.36)/(10- 1)= -9.42 so has equation V= -9.42(h- 1)+ 75.36. Setting that equal to 30 gives -9.42(h- 1)+ 75.36= 30 so h= 1+ (30- 75.36)/-9.42= 5.82. At h= 5.82, V= 29.95 which is less than 30 so we repeat with points (5, 75.36) and (5.82, 29.95).
"Newton's method" is more complicated but typically converged faster than the secant method and does not require finding two values of x on opposite sides of the root. Instead of taking a secant line between two points on the graph, we take the tangent line to the graph at one point. Given the equation f(h)= 0, the slope of the tangent line is f'(h). At point \(\displaystyle (h_0, f(h_0))\) the equation of the tangent line is \(\displaystyle V= f'(h_0)(h- h_0)+ f(h_0)\). Setting that equal to 0 we have \(\displaystyle f'(h_0)(h- h_0)+ f(h_0)= 0\) so \(\displaystyle h= h_0- \frac{f(h_0)}{f'(h_0)}\). Since Newton's method requires f(x)= 0, we take \(\displaystyle f(h)= 3\pi(9- h)- 30\). Since that is linear it has constant derivative \(\displaystyle f'(h)= -3\pi\). Newton's method then says that, from a given \(\displaystyle h_0\), we move to \(\displaystyle h= h_0- \frac{3\pi(9- h_0)- 30}{-3\pi}= h_0+ (9- h_0- \frac{30}{3\pi})= 5.82\). Which, again because the original equation is linear so Newton's method just reduces to that equation, is the correct answer.\)