SAT MATH! Sum of integer questions...

[wlkid9]

x = the sum of all odd integers from 1 to 49, inclusive

y = the sum of all even integers from 2 to 50, inclusive

z= the sum of alll integers from 1 to 48, inclusive

what is the value of x + y - z?

My friend told me that I should try 1 +49, then 3 + 47, 5 +45, and on. I noticed that of course every time you do this you get 50. I couldn't get far with this and just got huge numbers.

The answer is 99.

 

[galactus]

\(\displaystyle x=\sum_{k=1}^{25}(2k-1)\)

\(\displaystyle \sum_{k=1}^{n}(2k-1)=n^{2}\)

\(\displaystyle y=\sum_{k=1}^{25}(2k)\)

\(\displaystyle \sum_{k=1}^{n}2k=n(n+1)\)

\(\displaystyle z=\sum_{k=1}^{n}k=\frac{n(n+1)}{2}\)

 

[wlkid9]

Explanation?

 

[mmm4444bot]

Mathematics is all about patterns.

Can you "see" what's left when you subtract z away from x + y ?

(Double-click the image, to expand)

[attachment=0:1jnzp54o]Patterns.jpg[/attachment:1jnzp54o]

Oops, I just noticed that I missed a plus sign after the 49 (to add the line which is x to the line which is y), so let's say that the addition is implied (heh, heh).

 

[Mrspi]

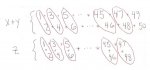
x = the sum of all odd integers from 1 to 49, inclusive

y = the sum of all even integers from 2 to 50, inclusive

z= the sum of alll integers from 1 to 48, inclusive

what is the value of x + y - z?

My friend told me that I should try 1 +49, then 3 + 47, 5 +45, and on. I noticed that of course every time you do this you get 50. I couldn't get far with this and just got huge numbers.

The answer is 99.

Well...if you are finding the sum of the odd integers from 1 to 49, you're adding 1 + 3 + 5 + 7 + ....+ 47 + 49

Pair them up...one from the left side, and one from the right side of this "list"

(1 + 49) + (3 + 47) + (5 + 45) + (7+ 43) + (9 + 41) you see that the sum of the numbers in each pair is 50? Now, think about how many pairs you'll have, each adding up to 50. Multiply the number of pairs by 50 to find the sum.

Your second question asks for the sum of the EVEN numbers from 2 to 50.....so you are dealing with these numbers...
2, 4, 6, 8, ....46, 48, 50

Note that if you pair up the numbers (first and last in the list), you'll have 2 + 50, or 52, and 4 + 48, or 52, and 6 + 46, or 52.....
How many pairs do you have which add up to 52? Multiply the number of pairs times 52 to find the sum.

Finally, you are asked to find z, or the sum of all the integers from 1 to 48.
1 + 2 + 3 + 4 + 5 + .....+ 45 + 46 + 47 + 48

Again, pair up the numbers. 1 + 48 = 49
2 + 47 = 49
3 + 46 = 49

How many pairs like this are there? If the numbers in each pair add up to 49, and you know how many pairs there are, it shouldn't be too difficult to find the sum.

When you have the answer to the first part (which is x) and the answer to the second part (which is y), it should be easy to find z...which is x + y.