You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Rule for Cancellation and Equals Sign?
- Thread starter gijas
- Start date
mmm4444bot
Super Moderator
- Joined
- Oct 6, 2005
- Messages
- 10,962
a complete description of the Cancellation rule
There are different situations in mathematics where stuff "cancels". There is no single rule to describe all of these situations. Please tell us what you're thinking about, when you write "cancellation rule".
what does the equal sign tell me? When it says … "this = that" what exactly is this telling me?
The equals sign appears in an equation.
An equation is a mathematical statement which says that the numerical value of the left-hand side IS THE SAME AS the numerical value of the right-hand side.
This statement (depending upon the particular equation) may be true or it may be false.
There are different situations in mathematics where stuff "cancels". There is no single rule to describe all of these situations. Please tell us what you're thinking about, when you write "cancellation rule".
I believe this means when you use the cancellation rule for rational expressions and equations (when you factor then eliminate like expressions)
Also, for the (equal = sign) explanation.. I found this definition that is similar BELOW. But your explanation sounds much more convincing as this is talking about equality in general but not related to the equation in particular.
Equality
Definition of Equality
More about Equality
- Equality is a state in which two things or values are always equal.
- In the state of equality, both values on the left and the right side of the sign ‘=’ will be the same.
- The equality “A is equal to B” is written as “A = B”.
- If a number is added on both sides of an equality, then the value of the expression or equation remains the same i.e. if c is any real number, then x + c = y + c
- If a number is subtracted from both sides of an equality, then the value of the expression or equation remains the same i.e. if c is any real number, then x - c = y - c
- If a number is multiplied on both sides of an equality, then the value of the expression or equation remains the same i.e. if c is any real number, then x · c = y · c.
- If a number divides both sides of an equality, then the value of the expression or equation remains same i.e. if c is any real number, then
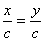
Last edited:
mmm4444bot
Super Moderator
- Joined
- Oct 6, 2005
- Messages
- 10,962
when you use the cancellation rule for rational expressions
(when you factor then eliminate like expressions)
That's pretty much the rule.
If you can factor out the same expression from both the numerator and the denominator, then you may cancel that factor above and below.
Have you seen an example or something that makes you think there is more to it? In other words, I'm curious to know why you ask about this rule.
That's pretty much the rule.
Have you seen an example or something that makes you think there is more to it? In other words, I'm curious to know why you ask about this rule.
No. I was just wanting a explanation of the cancellation rule not a example in otherwords. I think that is it though. If there is something more to it I have no clue.
See whether this helps.
\(\displaystyle \dfrac{a\cdot b}{a\cdot c} = \dfrac{a}{a}\cdot \dfrac{b}{c}\)
But anything (except zero) divided into itself equals 1 so
\(\displaystyle \dfrac{a}{a}\cdot \dfrac{b}{c} = 1\cdot \dfrac{b}{c}\)
And 1 times something equals that something so
\(\displaystyle 1\cdot \dfrac{b}{c} = \dfrac{b}{c}.\)
In short, rather than going through that every time, we say the a's cancel and go
\(\displaystyle \dfrac{a\cdot b}{a\cdot c} = \dfrac{b}{c}.\)
Does that help?
Looks good Jeff. Here's another question that has stumped me.
Explain the difference between
a) a factor "in" the numerator
b) a factor "of" the numerator
I assume in words rather than an example.
mmm4444bot
Super Moderator
- Joined
- Oct 6, 2005
- Messages
- 10,962
\(\displaystyle \dfrac{d + a\cdot b}{c}\).
a is a factor in the numerator
it is definitely wrong to say that a is a factor of the numerator
JeffM is exactly correct; this difference between "in" and "of" is the point of the exercise, I believe.
They could have avoided the ambiguity, by providing such an expression as Jeff's with the exercise.
