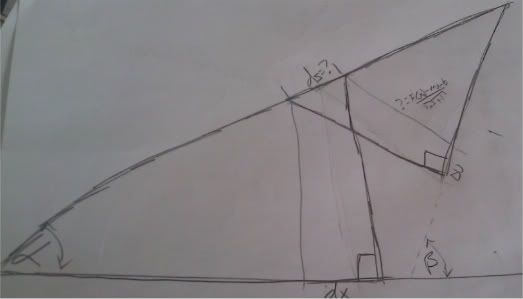
I do not believe a centroid was meant to be used here since we're only in section 7.2. But, use whatever works.
Note, the first part of the problem asks us to derive the formula for AREA.
So, here is the first part. This is probably the most involved part of the project.
Once this is shown, the volume formula can be derived easier.
The given hint suggests finding the area of the slanted approximating rectangle(s).
The height of the rectangle is the distance between a point and a line. The distance marked with a ? on the upper side of the rectangle. Call this length D
The formula for the distance between a point and a line is \(\displaystyle D=\frac{|Ax_{0}+By_{0}+C|}{\sqrt{A^{2}+B^{2}}}\)
In this case, our general line has standard equation \(\displaystyle -mx+y-b=0\)
Thus, the distance from point \(\displaystyle (x_{i}, y_{i})\) to the line y=mx+b is:
\(\displaystyle \boxed{D=\frac{f(x_{i})-mx-b}{\sqrt{m^{2}+1}}}\)
Now, the width of the rectangle at the other little question mark:
At the question mark we have the arc length of the tangent line to the curve C.
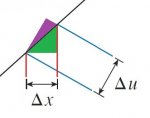
Call this ds. ds is often used for arc length. Make a right triangle with ds as the hypotenuse and dx as the base.
Using the arc length formula, \(\displaystyle \frac{ds}{dx}=\sqrt{1+[f'(x)]^{2}}\)
Now, make a triangle with ds as the hypoteneuse and du as the base this time.
Notice the angles \(\displaystyle \alpha, \;\ \beta\) down at the bottom of the diagram?.
They come in to play here. I hadn't noticed them at first, so I scratched my head a little longer than I should have.

\(\displaystyle \frac{du}{ds}=cos(\beta-\alpha)\)
Now, using the subtraction formula for cos, we get:
\(\displaystyle \frac{du}{ds}=cos(\beta-\alpha)=cos\beta cos\alpha+sin\beta sin\alpha\)
But \(\displaystyle tan\alpha=f'(x) \;\ (\text{slope of f(x)}), \;\ m=tan\beta \;\ (\text{slope of line y=mx+b})\)
Thus, \(\displaystyle \frac{ds}{dx}=sec\alpha=\sqrt{1+[f'(x)]^{2}}\)
We want \(\displaystyle \frac{du}{dx}=\frac{du}{ds}\cdot\frac{ds}{dx}\)
Divide du/ds by \(\displaystyle cos\alpha\) and we get:
\(\displaystyle \frac{du}{dx}=\frac{cos\beta cos\alpha+sin\beta sin\alpha}{cos\alpha}=\frac{1+tan\beta tan\alpha}{\sqrt{1+tan^{2}\beta}}=\frac{1+mf'(x)}{\sqrt{1+m^{2}}}\)
Now, the area of each rectangle is \(\displaystyle D\cdot\frac{du}{dx}\)
\(\displaystyle \left[\frac{f(x)-mx-b}{\sqrt{1+m^{2}}}\right]\left[\frac{1+mf'(x)}{\sqrt{1+m^{2}}}\right]\)
\(\displaystyle =\left[f(x)-mx-b\right]\left[\frac{1+mf'(x)}{m^{2}+1}\right]\)
Now, finally, add up all the rectangle area:
\(\displaystyle \frac{1}{m^{2}+1}\int_{p}^{q}\left[f(x)-mx-b\right]\left[1+mf'(x)\right]dx\)
The volume is found by rotating each rectangle and adding them up.
\(\displaystyle \pi\int D^{2}du\)