Right Triangle with 3-legs: Find measure of side AD, given

I

ILovePizza

New member
Joined
Jan 19, 2009
Messages
27
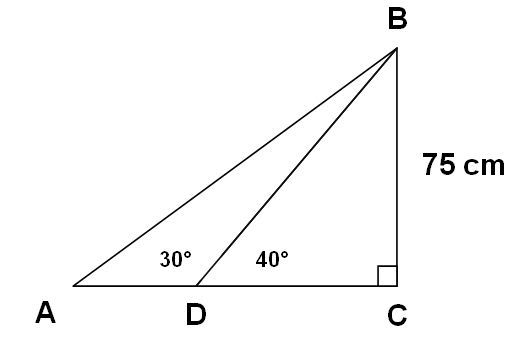
I’m just learning trigonometry, but we have already moved on to the law of sine, but I’m still having trouble with some Right Triangle problems like the one shown here.

I can do a simple Right Triangle, but I have no idea how to figure this problem out?

Thanks for your help in advance!

Find the measure of side AD.

Angle1.jpg
 
Re: Right Triangle with 3-legs

Well, you have 2 SIMPLE right triangles: ABC and DBC.
Do each one individually, calculating AC and DC.
Then AD is simply AC - DC : kapish?

AFTER you're finished, look up "30-60-90 right triangle" using google.
Should help you in future.
 
Re: Right Triangle with 3-legs

Thank you for the reply!
Where I get confused is with the 30, and 40 degrees.

I see the triangle for DBC, but do for ABC, do I use the 30degree, and a total of 30 + 70 for 100?

I’ll try DBC with just the 30 first:

(Find side b)

STEP ONE:
sin(Ø) = O = 75
---------- H---0

cos(Ø) = A = b
----------H ---0

tan(Ø) = O = 75 ****
---------- A--- b

STEP TWO:

tan(Ø) = tan(40) = 75 (nothing to cross multiple)
---------------1-------b

Rewrite: tan(40) x75 = 62.9324 (63) rounded to nearest 10th

---------------------------------------------------------------------

Next Part ABC (find side b)

sin(Ø) = O = 75
----------H----0

cos(Ø) = A = b
----------H---0

tan(Ø) = O = 75 ****
----------A----b

STEP TWO:

tan(Ø) = tan(30) = 75 ( nothing to cross multiple)
---------------1-------b

Rewrite: tan(30) x75 = 43.3012 (43) rounded to nearest 10th

---------------------------------------------------------------------

DBC – ABC = 63 - 43 = 20 cm

I'm not sure this right?
 
Re: Right Triangle with 3-legs

ILovePizza said:
I'm not sure this right?
Click to expand...
It is NOT. You do not seem to have grasped the basics.
Can't teach you the basics here; teacher/classroom needed.

Go here, and study the examples:
http://www.staff.vu.edu.au/mcaonline/un ... atios.html

Question:
Your problem indicates that you're expected to use the Law of Sines:
why are you complicating matters with Cos and Tan ?
 
Re: Right Triangle with 3-legs

I didn't think it was right; however, I'm off to school now, so I'll keep trying while there. Unfortunately, we don't have math today, so I can't ask the teacher.

I’m using sin, cos, tan, because this problem was under the chapter with Right Triangles, and pages away from the chapter where we are now beginning to learn the Law of sine. Others have figured this out, so I’ll ask around to see how they did it.

I’m a little disheartened that you’re giving up on me so soon, but I appreciate your efforts to help. When I figure this out, I’ll post the solution.

Off to learn (smile).
 
Re: Right Triangle with 3-legs

PS. I’ll try using the law of sine.
I’m hoping this method will be easier to grasp <grin>
 
I just figured it out (smile)

DC = 75/tan(40) = 89.3815 (89.4)

AC = 129.9

AC – DC = AD

129.9 – 89.4 = 40.5

AD = 40.5 (Yeah!!!)

And I did this using the sin, cos, tan method for Right Triangles.

Thank you...you spurred me on to attack this question. My only problem now is, I’m slightly late for school. Lets see if I can work an angle out for that problem (smile)!
 
Re: Right Triangle with 3-legs

ILovePizza said:
I’m a little disheartened that you’re giving up on me so soon...
Click to expand...
Not really "giving up"; much better for you to "get it yourself (as you did!)" than lead you by the hand :wink:

Good work: the whole site is proud of you!

To recap using "TAN":
AC = 75 / TAN(40)
CD = 75 / TAN(30)

AC - CD = 75 / TAN(40) - 75 / TAN(30) = 75 / [TAN(40) - TAN(30)] = 40.52229.....

Compliment: you have an excellent "math attitude".
Suggestion: change "ILovePizza" to "ILoveMath" :wink:
 
Thank you for your patience’s and confidence in my [lack-of <grn>] abilities.

I am curious about one thing that someone at school mentioned: Can you use the Cosine Law to solve a Right, and non-Right triangle?

I just thought if I could focus on one method to solve problems, it would be less confusing. But I am looking forward now to moving forward with trig; well, until the next problen anyway!
 
You must log in or register to reply here.
Top