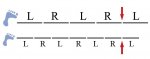Right Foot Forward
A short man takes three steps to a tall man's two steps. They both start out on the left foot. How many steps do they have to take before they are both stepping out on the right foot together?
Could anyone help me solve this? (detailed answer please)
A short man takes three steps to a tall man's two steps. They both start out on the left foot. How many steps do they have to take before they are both stepping out on the right foot together?
Could anyone help me solve this? (detailed answer please)